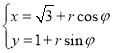题目内容
【题目】选修4-5：不等式选讲
设函数
.
（Ⅰ）求
的最小值及取得最小值时
的取值范围；
（Ⅱ）若集合
，求实数
的取值范围.
【答案】（1）3（2）
【解析】试题分析: （Ⅰ）利用绝对值三角不等式,求得
的最小值,以及取得最小值时x的取值范围; （Ⅱ）当集合
,函数
恒成立,即
的图象恒位于直线
的上方,数形结合求得a的取值范围.
试题解析:解：（Ⅰ）∵ 函数
，
当且仅当
，即
时
函数
的最小值为
．
（Ⅱ）函数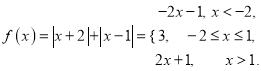
而函数
表示过点
，斜率为
的一条直线，
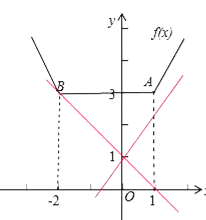
如图所示：当直线
过点
时， 
，∴
，
当直线
过点
时， 
，∴
，
故当集合
，函数
恒成立，
即
的图象恒位于直线
的上方，
数形结合可得要求的
的范围为
．
点睛: 两数和差的绝对值的性质: 
,特别注意此式，它是和差的绝对值与绝对值的和差性质，应用此式来求某些函数的最值时一定要注意等号成立的条件.恒成立问题的解决方法:(1)f(x)<m恒成立，须有[f(x)]max<m；(2)f(x)>m恒成立，须有[f(x)]min>m；(3)不等式的解集为R，即不等式恒成立；(4)不等式的解集为，即不等式无解．
练习册系列答案
一本好题口算题卡系列答案
相关题目
