题目内容
已知函数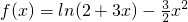 .
.
(1)求f(x)在[0,1]上的单调区间;
(2)若对任意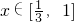 ,不等式|a-f(x)|>ln5,求实数a的取值范围.
,不等式|a-f(x)|>ln5,求实数a的取值范围.
解:(1)函数f(x)的定义域为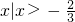 ,
, (3分)
(3分)
∴在[0,1]上,当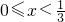 时,f'(x)>0时,f(x)单调递增;
时,f'(x)>0时,f(x)单调递增;
当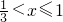 时,f'(x)<0,f(x)单调递减.
时,f'(x)<0,f(x)单调递减.
∴f(x)在[0,1]上的增区间是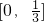 ,减区间是
,减区间是 .(开闭均可)(6分)
.(开闭均可)(6分)
(2)由|a-f(x)|>ln5,可得a-f(x)>ln5或a-f(x)<-ln5,
即a>f(x)+ln5或a<f(x)-ln5.(7分)
由(1)当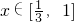 时,f(x)max=f(
时,f(x)max=f( )=ln3-
)=ln3- ,
,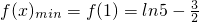 .(9分)
.(9分)
∵a>f(x)+ln5恒成立,∴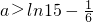 ,
,
∵a<f(x)-ln5恒成立,∴ .
.
∴a的取值范围为: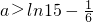 或
或 (12分)
(12分)
分析:(1)先求函数f(x)的定义域,然后求出导函数f'(x),在[0,1]上,求解不等式fˊ(x)>0和fˊ(x)<0即可求出函数f(x)的单调性;
(2)先将不等式的绝对值去掉得到a>f(x)+ln5或a<f(x)-ln5在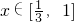 恒成立,然后建立不等式,解之即可求出a的取值范围.
恒成立,然后建立不等式,解之即可求出a的取值范围.
点评:本题主要考查利用导数研究函数的单调性,以及函数的性质、图象及导数等基础知识,考查灵活运用分类讨论的思想方法进行探索、分析与解决问题的综合能力,属于中档题.
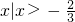 ,
, (3分)
(3分)∴在[0,1]上,当
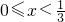 时,f'(x)>0时,f(x)单调递增;
时,f'(x)>0时,f(x)单调递增;当
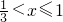 时,f'(x)<0,f(x)单调递减.
时,f'(x)<0,f(x)单调递减.∴f(x)在[0,1]上的增区间是
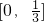 ,减区间是
,减区间是 .(开闭均可)(6分)
.(开闭均可)(6分)(2)由|a-f(x)|>ln5,可得a-f(x)>ln5或a-f(x)<-ln5,
即a>f(x)+ln5或a<f(x)-ln5.(7分)
由(1)当
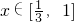 时,f(x)max=f(
时,f(x)max=f( )=ln3-
)=ln3- ,
,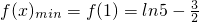 .(9分)
.(9分)∵a>f(x)+ln5恒成立,∴
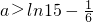 ,
,∵a<f(x)-ln5恒成立,∴
 .
.∴a的取值范围为:
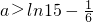 或
或 (12分)
(12分)分析:(1)先求函数f(x)的定义域,然后求出导函数f'(x),在[0,1]上,求解不等式fˊ(x)>0和fˊ(x)<0即可求出函数f(x)的单调性;
(2)先将不等式的绝对值去掉得到a>f(x)+ln5或a<f(x)-ln5在
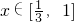 恒成立,然后建立不等式,解之即可求出a的取值范围.
恒成立,然后建立不等式,解之即可求出a的取值范围.点评:本题主要考查利用导数研究函数的单调性,以及函数的性质、图象及导数等基础知识,考查灵活运用分类讨论的思想方法进行探索、分析与解决问题的综合能力,属于中档题.

练习册系列答案
相关题目
 .
. .
. 的图象在x轴上方?
的图象在x轴上方? .
. 为f(x)的一个零点,求sin2x的值.
为f(x)的一个零点,求sin2x的值.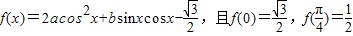 .
. .
. ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.