题目内容
已知曲线C:xy=1,过C上一点An(xn,yn)作一斜率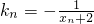 的直线交曲线C于另一点An+1(xn+1,yn+1).
的直线交曲线C于另一点An+1(xn+1,yn+1).
(1)求xn与xn+1之间的关系式;
(2)若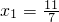 ,求证:数列
,求证:数列 是等比数列;
是等比数列;
(3)求证:(-1)x1+(-1)2x2+(-1)3x3+…(-1)nxn<1(n∈N*)
(1)解:∵C上一点An(xn,yn)作一斜率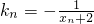 的直线交曲线C于另一点An+1(xn+1,yn+1).
的直线交曲线C于另一点An+1(xn+1,yn+1).
∴kn= =
= =-
=- =
=
∴xnxn+1=xn+2,即:xn+1=1+ .
.
(2)证明:设 ,由(1)得
,由(1)得 =
= =-2(
=-2( )=-2an
)=-2an
∵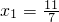 ,∴
,∴ =-2,∴数列{
=-2,∴数列{ }是以2为首项,2为公比的等比数列;
}是以2为首项,2为公比的等比数列;
(3)证明:由(2)得
∴
∴
∴(-1)n-1xn-1+(-1)nxn= <
< =
= +
+
当n为偶数时,则(-1)x1+(-1)2x2+…+(-1)nxn< +
+ +…+
+…+ =1-
=1- <1;
<1;
当n为奇数时,前n-1项为偶数项,
于是有:(-1)x1+(-1)2x2+…+(-1)nxn<1+(-1)nxn,而
∴1+(-1)nxn=1-xn<1
∴(-1)x1+(-1)2x2+…+(-1)nxn<1
综上所述,当n∈N*时,(-1)x1+(-1)2x2+…+(-1)nxn<1成立.
分析:(1)利用C上一点An(xn,yn)作一斜率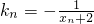 的直线交曲线C于另一点An+1(xn+1,yn+1),求出斜率,即可得到xn与xn+1之间的关系式;
的直线交曲线C于另一点An+1(xn+1,yn+1),求出斜率,即可得到xn与xn+1之间的关系式;
(2)设 ,由(1)得
,由(1)得 =-2an,从而可得数列{
=-2an,从而可得数列{ }是等比数列;
}是等比数列;
(3)先确定 ,证明(-1)n-1xn-1+(-1)nxn<
,证明(-1)n-1xn-1+(-1)nxn< +
+ ,再分类讨论,即可证得结论.
,再分类讨论,即可证得结论.
点评:本题考查了数列的递推式,考查等比数列的证明,考查证明不等式,考查了学生推理能力和基本的运算能力.
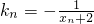 的直线交曲线C于另一点An+1(xn+1,yn+1).
的直线交曲线C于另一点An+1(xn+1,yn+1).∴kn=
 =
= =-
=- =
=
∴xnxn+1=xn+2,即:xn+1=1+
 .
.(2)证明:设
 ,由(1)得
,由(1)得 =
= =-2(
=-2( )=-2an
)=-2an∵
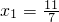 ,∴
,∴ =-2,∴数列{
=-2,∴数列{ }是以2为首项,2为公比的等比数列;
}是以2为首项,2为公比的等比数列;(3)证明:由(2)得

∴

∴

∴(-1)n-1xn-1+(-1)nxn=
 <
< =
= +
+
当n为偶数时,则(-1)x1+(-1)2x2+…+(-1)nxn<
 +
+ +…+
+…+ =1-
=1- <1;
<1;当n为奇数时,前n-1项为偶数项,
于是有:(-1)x1+(-1)2x2+…+(-1)nxn<1+(-1)nxn,而

∴1+(-1)nxn=1-xn<1
∴(-1)x1+(-1)2x2+…+(-1)nxn<1
综上所述,当n∈N*时,(-1)x1+(-1)2x2+…+(-1)nxn<1成立.
分析:(1)利用C上一点An(xn,yn)作一斜率
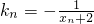 的直线交曲线C于另一点An+1(xn+1,yn+1),求出斜率,即可得到xn与xn+1之间的关系式;
的直线交曲线C于另一点An+1(xn+1,yn+1),求出斜率,即可得到xn与xn+1之间的关系式;(2)设
 ,由(1)得
,由(1)得 =-2an,从而可得数列{
=-2an,从而可得数列{ }是等比数列;
}是等比数列;(3)先确定
 ,证明(-1)n-1xn-1+(-1)nxn<
,证明(-1)n-1xn-1+(-1)nxn< +
+ ,再分类讨论,即可证得结论.
,再分类讨论,即可证得结论.点评:本题考查了数列的递推式,考查等比数列的证明,考查证明不等式,考查了学生推理能力和基本的运算能力.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目