Question

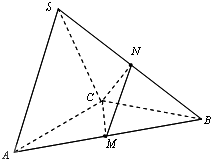
在三棱锥S-ABC中，△ABC是边长为2

3

的正三角形，平面SAC⊥平面ABC，SA=SC=2，M、N分别为AB、SB的中点．
（1）证明：AC⊥SB；
（2）求三棱锥B-CMN的体积．

Answer 1

（1）证明：取AC中点D，连接SD，DB．
因为SA=SC，AB=BC，所以AC⊥SD且AC⊥BD，
因为SD∩BD=D，所以AC⊥平面SDB．
又SB?平面SDB，所以AC⊥SB；
（2）因为AC⊥平面SDB，AC?平面ABC，所以平面SDC⊥平面ABC．
过N作NE⊥BD于E，则NE⊥平面ABC，
因为平面SAC⊥平面ABC，SD⊥AC，所以SD⊥平面ABC．
又因为NE⊥平面ABC，所以NE∥SD．
由于SN=NB，所以NE=

1

2

SD=

1

2

所以S_△CMB=

1

2

CM•BM=

3 3

2

所以V_B-CMN=V_N-CMB=

1

3

S_△CMB•NE=

1

3

×

3 3

2

×

1

2

=

3

4