Question

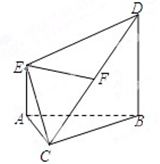
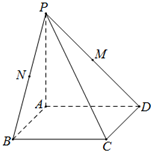
如图在四棱锥P-ABCD中，底面ABCD是正方形，PA⊥底面ABCD，垂足为点A，PA=AB=2，点M，N分别是PD，PB的中点．
（I）求证：PB∥平面ACM；
（II）求证：MN⊥平面PAC；
（III）求四面体A-MBC的体积．

Answer 1

证明：（I）连接AC，BD，AM，MC，MO，MN，且AC∩BD=O
∵点O，M分别是PD，BD的中点
∴MO∥PB，
∵PB?平面ACM，MO?平面ACM
∴PB∥平面ACM．…（4分）
（II）∵PA⊥平面ABCD，BD?平面ABCD
∴PA⊥BD
∵底面ABCD是正方形，∴AC⊥BD
又∵PA∩AC=A
∴BD⊥平面PAC…（7分）
在△PBD中，点M，N分别是PD，PB的中点，∴MN∥BD
∴MN⊥平面PAC．…（9分）
（III）∵VA-MBC=VM-ABC=

1

3

•S△ABC•h，h=

1

2

PA…（12分）
∴VA-MBC=

1

3

•

1

2

•AB•AD•

1

2

•PA=

2

3

．…（14分）