题目内容
已知函数
(1)若实数 求函数
求函数 在
在 上的极值;
上的极值;
(2)记函数 ,设函数
,设函数 的图像
的图像 与
与 轴交于
轴交于 点,曲线
点,曲线 在
在 点处的切线与两坐标轴所围成图形的面积为
点处的切线与两坐标轴所围成图形的面积为 则当
则当 时,求
时,求 的最小值.
的最小值.
解:(1)
当 时,由
时,由
若 ,则
,则 ,所以
,所以 恒成立,
恒成立,
所以 单调递增,无极值.
单调递增,无极值.
若 ,则
,则 单调递减;
单调递减;
 单调递增.
单调递增.
所以 有极小值
有极小值 .
.
(2) =
= 令
令 得
得 ,即
,即
 点处切线斜率:
点处切线斜率:
 点处切线方程:
点处切线方程:
令 得
得 ,令
,令 得
得
所以
令

当且仅当

练习册系列答案
相关题目
 在
在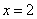 处有极大值.
处有极大值. 的值;
的值;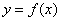 相切,求
相切,求 的取值范围;
的取值范围; 时,函数
时,函数 的下方,求
的下方,求 ,且
,且 ,则
,则 的值为 .
的值为 .  为函数
为函数 的
的
 阶导函数,即
阶导函数,即
 .若
.若 且集合
且集合 ,则集合
,则集合 中元素的个数为( )
中元素的个数为( ) (B)
(B)
 (D)
(D)
 行有
行有 ,每个数是它下一行左右相邻两数的和,如:
,每个数是它下一行左右相邻两数的和,如: …,则第
…,则第 行第3个数字是 .(用含
行第3个数字是 .(用含 的式子作答)
的式子作答)
 在点M处的切线斜率为3,则点M的坐标为( )
在点M处的切线斜率为3,则点M的坐标为( ) B.
B.  C.
C.  D.
D. 
 的单调递减区间为________.
的单调递减区间为________. 满足
满足 ,则
,则 .
.