题目内容
若a,b都是实数,则“a-b>0”是“a3-b3>0”的( )A.充分而不必要条件
B.必要而不充分条件
C.充分必要条件
D.既不充分也不必要条件
【答案】分析:根据立方差公式以及[(a-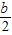 )2+
)2+ b2]≥0,由“a3-b3>0”可推出“a-b>0”成立,由“a-b>0”能推出“a3-b3>0”成立,从而得出结论.
b2]≥0,由“a3-b3>0”可推出“a-b>0”成立,由“a-b>0”能推出“a3-b3>0”成立,从而得出结论.
解答:解:由于 a3-b3=(a-b)(a2+ab+b2)=(a-b)[(a-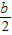 )2+
)2+ b2],且[(a-
b2],且[(a-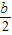 )2+
)2+ b2]≥0,
b2]≥0,
故由“a3-b3>0”可得 a-b>0,故必要性成立.
由“a-b>0”,一定能推出a3-b3=(a-b)[(a-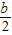 )2+
)2+ b2]>0成立,故充分性成立.
b2]>0成立,故充分性成立.
故“a-b>0”是“a3-b3>0”的充要条件,
故选C.
点评:本题主要考查充分条件、必要条件、充要条件的定义,立方差公式的应用,属于基础题.
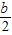 )2+
)2+ b2]≥0,由“a3-b3>0”可推出“a-b>0”成立,由“a-b>0”能推出“a3-b3>0”成立,从而得出结论.
b2]≥0,由“a3-b3>0”可推出“a-b>0”成立,由“a-b>0”能推出“a3-b3>0”成立,从而得出结论.解答:解:由于 a3-b3=(a-b)(a2+ab+b2)=(a-b)[(a-
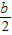 )2+
)2+ b2],且[(a-
b2],且[(a-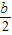 )2+
)2+ b2]≥0,
b2]≥0,故由“a3-b3>0”可得 a-b>0,故必要性成立.
由“a-b>0”,一定能推出a3-b3=(a-b)[(a-
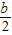 )2+
)2+ b2]>0成立,故充分性成立.
b2]>0成立,故充分性成立.故“a-b>0”是“a3-b3>0”的充要条件,
故选C.
点评:本题主要考查充分条件、必要条件、充要条件的定义,立方差公式的应用,属于基础题.

练习册系列答案
相关题目