题目内容
设f(x)=kx3+3(k-1)x2-k2+1在区间(0,3)是增函数,则k的取值范围是
- A.k<0
- B.0<k≤1
- C.k≥1
- D.k≤1
C
分析:先求导函数f'(x),函数f(x)=kx3+3(k-1)x2-k2+1在区间(0,3)上是减函数转化成f'(x)≥0在区间(0,3)上恒成立,讨论k的符号,从而求出所求.
解答:f'(x)=3kx2+6(k-1)x,
∵函数f(x)=kx3+3(k-1)x2-k2+1在区间(0,3)上是增函数,
∴f'(x)=3kx2+6(k-1)x≥0在区间(0,3)上恒成立
当k=0时,f'(x)=-6<0,显然不成立;
当k>0时,由于二次函数y=3kx2+6(k-1)x,开口向上,始终过原点,对称轴为x=-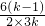 =
=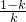 ,
,
只有当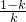 ≤0,才满足3kx2+6(k-1)x≥0在区间(0,3)上恒成立,解得k≥1;
≤0,才满足3kx2+6(k-1)x≥0在区间(0,3)上恒成立,解得k≥1;
当k<0时,由于二次函数y=3kx2+6(k-1)x,开口向下,始终过原点,对称轴为x=-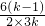 =
=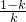 ,
,
只有当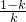 ≥0,且f'(3)≥0,时才满足,解得此时k
≥0,且f'(3)≥0,时才满足,解得此时k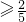 ,显然与k<0矛盾,故应舍去.
,显然与k<0矛盾,故应舍去.
综上,可知k≥1
故选C.
点评:本题主要考查导函数的正负与原函数的单调性之间的关系,同时考查了分析与解决问题的综合能力,属于中档题.
分析:先求导函数f'(x),函数f(x)=kx3+3(k-1)x2-k2+1在区间(0,3)上是减函数转化成f'(x)≥0在区间(0,3)上恒成立,讨论k的符号,从而求出所求.
解答:f'(x)=3kx2+6(k-1)x,
∵函数f(x)=kx3+3(k-1)x2-k2+1在区间(0,3)上是增函数,
∴f'(x)=3kx2+6(k-1)x≥0在区间(0,3)上恒成立
当k=0时,f'(x)=-6<0,显然不成立;
当k>0时,由于二次函数y=3kx2+6(k-1)x,开口向上,始终过原点,对称轴为x=-
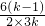 =
=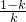 ,
,只有当
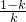 ≤0,才满足3kx2+6(k-1)x≥0在区间(0,3)上恒成立,解得k≥1;
≤0,才满足3kx2+6(k-1)x≥0在区间(0,3)上恒成立,解得k≥1;当k<0时,由于二次函数y=3kx2+6(k-1)x,开口向下,始终过原点,对称轴为x=-
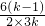 =
=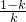 ,
,只有当
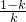 ≥0,且f'(3)≥0,时才满足,解得此时k
≥0,且f'(3)≥0,时才满足,解得此时k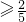 ,显然与k<0矛盾,故应舍去.
,显然与k<0矛盾,故应舍去.综上,可知k≥1
故选C.
点评:本题主要考查导函数的正负与原函数的单调性之间的关系,同时考查了分析与解决问题的综合能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设函数f(x)=kx3+3(k-1)x2-k2+1在区间(0,4)上是减函数,则k的取值范围( )
A、k<
| ||
B、0<k≤
| ||
C、0≤k≤
| ||
D、k≤
|