题目内容
设f(x)=
的反函数为f-1(x),若f-1(-
)=n,则f(n+4)=( )
|
|
| 8 |
| 9 |
| A、2 | B、-2 | C、1 | D、-1 |
分析:根据反函数的定义,若f-1(-
)=n,则f(n)=-
由此方程求出n,再求f(n+4)的值.
| 8 |
| 9 |
| 8 |
| 9 |
解答:解:由题 意可得f(n)=-
若3n-6-1=-
解得n=4符合题意
若-log3n+1=-
,解得n=3
-1<3故不合题意,
综上知n=4
故f(8)=-log39=-2
故选B
| 8 |
| 9 |
若3n-6-1=-
| 8 |
| 9 |
若-log3n+1=-
| 8 |
| 9 |
| 8 |
| 9 |
综上知n=4
故f(8)=-log39=-2
故选B
点评:本题考查反函数的性质,根据反函数的性质把求函数值的问题转化为求自变量的问题,从而达到简化解题的目的,用到了转化的思想,做题时根据情况灵活转化,是解题成功的法宝.

练习册系列答案
相关题目
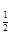 (
(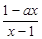 )为奇函数,a为常数.
)为奇函数,a为常数.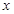 的值,不等式
的值,不等式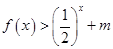 恒成立,求实数
恒成立,求实数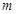 的取值范围.
的取值范围.
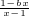 为奇函数,b为常数.
为奇函数,b为常数. )x+m恒成立,求实数m的取值范围.
)x+m恒成立,求实数m的取值范围.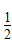
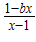 为奇函数,b为常数.
为奇函数,b为常数. )x+m恒成立,求实数m的取值范围.
)x+m恒成立,求实数m的取值范围.