题目内容

函数y=f（x）与直线x=t的交点个数为

A.
有且只有一个
B.
至多一个
C.
至少一个
D.
无数多个

B
分析：由函数的定义可得，当x在定义域内任取一个值，都有唯一的一个函数值与它对应，当x的取值不在定义域内时，
就没有函数值和它对应，由此得出结论．
解答：由函数的定义可得，当x在定义域内任取一个值，都有唯一的一个函数值与它对应，
当x的取值不在定义域内时，就没有函数值和它对应，
故函数y=f（x）的图象与直线x=t的交点个数至多有一个，
故选B．
点评：本题主要考查函数的定义，属于基础题．

练习册系列答案

快乐大本营单元练习测试系列答案

快乐天天练神算手系列答案

快乐学习检测卷系列答案

快乐学习随堂练系列答案

快速课课通系列答案

李庚南初中数学自选作业系列答案

大儒教育练测考系列答案

亮点给力考点激活系列答案

领航中考系列答案

领跑中考系列答案

相关题目

若y=f（x）是R上的函数，则函数y=f（2x）与y=f（1-2x）的图象关直

下列命题：
（1）如果平面γ与两个平面α、β所成的二面角都是直二面角，则α∥β．
（2）函数y=sinx在第一象限是增函数．
（3）函数y=tg

的最小正周期是π．
（4）奇函数y=f（x）在定义域R上满足f（1+x）=f（1-x），则y=f（x）是以4为周期的周期函数．
其中正确命题的序号是

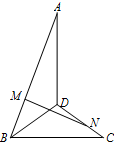直二面角A-BD-C中，M、N分别是线段AB、CD上的点（不包括端点），且∠ADB=∠DBC=90°，AD=DB=BC=1，AM=DN，AM=x，MN=y．
（1）若MN与平面BCD所成的角为45°，求x的值；
（2）求函数y=f（x）的解析式及定义域、值域．

给出下列五个命题：
①通项公式为a_n=a₁•2^n-1的数列是首项为a₁公比为2的等比数列；
②有两个侧面同时与底面垂直的棱柱一定是直棱柱；
③直线y=x•tanθ+1的倾斜角是θ；
④函数y=f（x）（x∈R）的值域是集合A，则函数y=f（-2x+1）（x∈R）的值域也是A；
⑤正方体的内切球与其外接球的表面积之比为1：3．其中正确命题的编号是

下列命题：
（1）如果平面γ与两个平面α、β所成的二面角都是直二面角，则α∥β．
（2）函数y=sinx在第一象限是增函数．
（3）函数y=tg

的最小正周期是π．
（4）奇函数y=f（x）在定义域R上满足f（1+x）=f（1-x），则y=f（x）是以4为周期的周期函数．
其中正确命题的序号是．