题目内容
已知a,b∈R*,如果a, ,b成等差数列,则
,b成等差数列,则 +
+ 的最小值是
的最小值是
- A.1
- B.2
- C.3
- D.4
D
分析:先根据等差中项的含义得到a+b=1,再由 +
+ =(
=( +
+ )×1=(
)×1=( +
+ )(a+b),然后展开再由基本不等式可求得最小值.
)(a+b),然后展开再由基本不等式可求得最小值.
解答:∵a, ,b成等差数列∴a+b=1
,b成等差数列∴a+b=1
∴ +
+ =(
=( +
+ )(a+b)=2+
)(a+b)=2+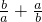 ≥2+2
≥2+2 =2+2=4
=2+2=4
当且仅当a=b= 时等号成立,
时等号成立,
故 +
+ 的最小值是4
的最小值是4
故选D.
点评:本题主要考查等差中项的含义和基本不等式的应用.考查基础知识 的综合应用.基本不等式在解决最值问题时应用比较广泛,一定要注意其要满足的“一正、二定、三相等”条件.
分析:先根据等差中项的含义得到a+b=1,再由
 +
+ =(
=( +
+ )×1=(
)×1=( +
+ )(a+b),然后展开再由基本不等式可求得最小值.
)(a+b),然后展开再由基本不等式可求得最小值.解答:∵a,
 ,b成等差数列∴a+b=1
,b成等差数列∴a+b=1∴
 +
+ =(
=( +
+ )(a+b)=2+
)(a+b)=2+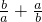 ≥2+2
≥2+2 =2+2=4
=2+2=4当且仅当a=b=
 时等号成立,
时等号成立,故
 +
+ 的最小值是4
的最小值是4故选D.
点评:本题主要考查等差中项的含义和基本不等式的应用.考查基础知识 的综合应用.基本不等式在解决最值问题时应用比较广泛,一定要注意其要满足的“一正、二定、三相等”条件.

练习册系列答案
相关题目

 如图,已知A、B为椭圆
如图,已知A、B为椭圆 选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分. 选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分.
选做题在A、B、C、D四小题中只能选做2题,每小题10分,共计20分. ]所对应的变换把直线l:2x-y=3变换为自身,求a,b的值.
]所对应的变换把直线l:2x-y=3变换为自身,求a,b的值. t为参数)化为普通方程.
t为参数)化为普通方程. )≥92.
)≥92. ]所对应的变换把直线l:2x-y=3变换为自身,求a,b的值.
]所对应的变换把直线l:2x-y=3变换为自身,求a,b的值. t为参数)化为普通方程.
t为参数)化为普通方程. )(2b+
)(2b+ )≥92.
)≥92.