题目内容
已知椭圆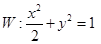 ,直线
,直线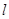 与
与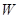 相交于
相交于 、
、 两点,
两点,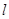 与
与 轴、
轴、 轴分别相交于
轴分别相交于 、
、 两点,
两点, 为坐标原点.
为坐标原点.
(1)若直线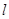 的方程为
的方程为 ,求
,求 外接圆的方程;
外接圆的方程;
(2)判断是否存在直线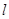 ,使得
,使得 、
、 是线段
是线段 的两个三等分点,若存在,求出直线
的两个三等分点,若存在,求出直线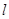 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(1) ;(2)存在,且直线
;(2)存在,且直线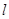 的方程为
的方程为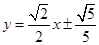 或
或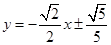 .
.
解析试题分析:(1)先确定 三个顶点的坐标,利用其外接圆圆心即为该三角形垂直平分线的交点求出外接圆的圆心,并利用两点间的距离公式求出外接圆的半径,从而求出外接圆的方程;(2)将
三个顶点的坐标,利用其外接圆圆心即为该三角形垂直平分线的交点求出外接圆的圆心,并利用两点间的距离公式求出外接圆的半径,从而求出外接圆的方程;(2)将 、
、 是线段
是线段 的两个三等分点等价转化为线段
的两个三等分点等价转化为线段 的中点与线段
的中点与线段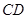 的中点重合,且有
的中点重合,且有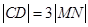 ,借助韦达定理与弦长公式进行求解.
,借助韦达定理与弦长公式进行求解.
试题解析:(1)因为直线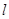 的方程为
的方程为 ,
,
所以 轴的交点
轴的交点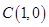 ,与
,与 轴的交点
轴的交点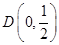 .
.
则线段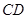 的中点
的中点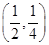 ,
,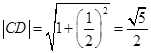 ,
,
即 外接圆的圆心为
外接圆的圆心为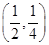 ,半径为
,半径为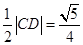 ,
,
所以 外接圆的方程为
外接圆的方程为 ;
;
(2)结论:存在直线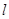 ,使得
,使得 、
、 是线段
是线段 的两个三等分点.
的两个三等分点.
理由如下:
由题意,设直线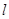 的方程为
的方程为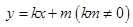 ,
,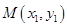 ,
,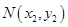 ,
,
则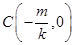 ,
,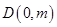 ,
,
由方程组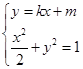 得
得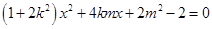 ,
,
所以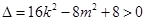 ,(*)
,(*)
由韦达定理,得 ,
,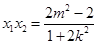 .
.
由 、
、 是线段
是线段 的两个三等分点,得线段
的两个三等分点,得线段 的中点与线段
的中点与线段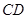 的中点重合.
的中点重合.
所以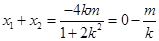 ,
,
解得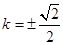 .
.
由 、
、 是线段
是线段 的两个三等分点,得
的两个三等分点,得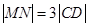 .
.
所以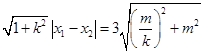 ,
,
即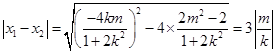 ,
,
解得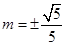 .
.
验证知(*)成立.
所以存在直线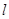 ,使得
,使得 、
、 是线段
是线段 的两个三等分点,此时直线l的方程为
的两个三等分点,此时直线l的方程为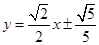 ,
,
或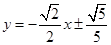 .
.
考点:1.三角形的外接圆方程;2.韦达定理;3.弦长公式

练习册系列答案
相关题目
 的抛物线
的抛物线 的焦点
的焦点 与椭圆
与椭圆 的右焦点重合,
的右焦点重合, 在第一和第四象限的交点分别为
在第一和第四象限的交点分别为 .
. 是边长为
是边长为 的正三角形,求抛物线
的正三角形,求抛物线 ,求椭圆
,求椭圆 .
.
 ,求点A的坐标;
,求点A的坐标;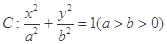 的离心率为
的离心率为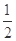 ,以原点
,以原点 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线 相切。
相切。 的标准方程;
的标准方程;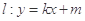 与椭圆
与椭圆 、
、 两点,且
两点,且 ,试判断
,试判断 的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.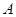 、
、 、
、 是长轴长为
是长轴长为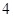 的椭圆
的椭圆 上的三点,点
上的三点,点 过椭圆中心
过椭圆中心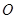 ,且
,且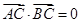 ,
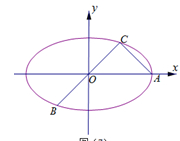
,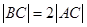 .
.
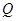 ,使得
,使得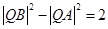 ?若存在,有几个(不必求出
?若存在,有几个(不必求出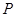 ,作圆
,作圆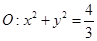 的两条线,切点分别为
的两条线,切点分别为 、
、 ,,若直线
,,若直线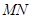 在
在 轴、
轴、 轴上的截距分别为
轴上的截距分别为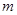 、
、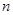 ,证明:
,证明: 为定值.
为定值. 的短半轴长为
的短半轴长为 ,动点
,动点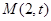
 在直线
在直线 (
( 为半焦距)上.
为半焦距)上. 为直径且被直线
为直径且被直线 截得的弦长为
截得的弦长为 的圆的方程;
的圆的方程;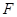 是椭圆的右焦点,过点
是椭圆的右焦点,过点 ,
, 的长为定值,并求出这个定值.
的长为定值,并求出这个定值.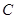 的中心在原点,右焦点为
的中心在原点,右焦点为 ,渐近线方程为
,渐近线方程为 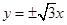 .
.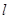 :
: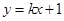 与双曲线
与双曲线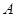 、
、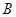 两点,问:当
两点,问:当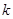 为何值时,以
为何值时,以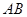 为直径的圆过原点;
为直径的圆过原点;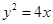 .
.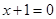 相切,求所有的圆都经过的定点坐标;
相切,求所有的圆都经过的定点坐标;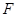 ,若过
,若过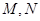 两点,若
两点,若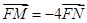 ,求直线
,求直线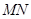 的斜率;
的斜率;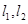 ,抛物线与
,抛物线与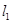 交于点
交于点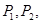 与
与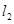 交于点
交于点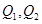 .
.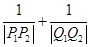 为一常数.
为一常数. =1(a>0,b>0)的一个焦点,并与双曲线实轴垂直,已知拋物线与双曲线的一个交点为
=1(a>0,b>0)的一个焦点,并与双曲线实轴垂直,已知拋物线与双曲线的一个交点为 ,求拋物线与双曲线方程.
,求拋物线与双曲线方程.