题目内容
在△ABC中,内角A,B,C的对边边长分别为a,b,c,且 .若c=10,则△ABC的面积是________.
.若c=10,则△ABC的面积是________.
24
分析:由题意得acosA=bcosB,结合正弦定理化简得sin2A=sin2B,所以2A=2B或2A+2B=180°.由于a、b不相等,得A≠B,因此A+B=90°,可得△ABC是直角三角形.根据c=10和 ,利用勾股定理算出b=6且a=8,即可得到△ABC的面积.
,利用勾股定理算出b=6且a=8,即可得到△ABC的面积.
解答:∵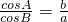 ,∴acosA=bcosB,结合正弦定理得sinAcosA=sinBcosB
,∴acosA=bcosB,结合正弦定理得sinAcosA=sinBcosB
∴2sinAcosA=2sinBcosB,即sin2A=sin2B
∵A、B是三角形的内角
∴2A=2B或2A+2B=180°,可得A=B或A+B=90°
∵ ,得a、b的长度不相等
,得a、b的长度不相等
∴A=B不成立,只有A+B=90°,可得C=180°-(A+B)=90°
因此,△ABC是直角三角形
设b=3x,a=4x,可得c= =5x=10
=5x=10
∴x=2,于是b=6且a=8,
由此可得△ABC的面积是S= ab=
ab= ×8×6=24
×8×6=24
故答案为:24
点评:本题给出△ABC的边角关系,叫我们判断三角形的形状并求三角形的面积,着重考查了利用正弦定理解三角形、诱导公式和二倍角正弦的公式等知识,属于中档题.
分析:由题意得acosA=bcosB,结合正弦定理化简得sin2A=sin2B,所以2A=2B或2A+2B=180°.由于a、b不相等,得A≠B,因此A+B=90°,可得△ABC是直角三角形.根据c=10和
 ,利用勾股定理算出b=6且a=8,即可得到△ABC的面积.
,利用勾股定理算出b=6且a=8,即可得到△ABC的面积.解答:∵
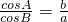 ,∴acosA=bcosB,结合正弦定理得sinAcosA=sinBcosB
,∴acosA=bcosB,结合正弦定理得sinAcosA=sinBcosB∴2sinAcosA=2sinBcosB,即sin2A=sin2B
∵A、B是三角形的内角
∴2A=2B或2A+2B=180°,可得A=B或A+B=90°
∵
 ,得a、b的长度不相等
,得a、b的长度不相等∴A=B不成立,只有A+B=90°,可得C=180°-(A+B)=90°
因此,△ABC是直角三角形
设b=3x,a=4x,可得c=
 =5x=10
=5x=10∴x=2,于是b=6且a=8,
由此可得△ABC的面积是S=
 ab=
ab= ×8×6=24
×8×6=24故答案为:24
点评:本题给出△ABC的边角关系,叫我们判断三角形的形状并求三角形的面积,着重考查了利用正弦定理解三角形、诱导公式和二倍角正弦的公式等知识,属于中档题.

练习册系列答案
相关题目