题目内容
已知函数![]() ,其中
,其中![]()
![]() .
.
(Ⅰ)判断函数![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(Ⅱ)设![]() =-4,且
=-4,且![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
解:(I)若![]() 即
即![]() ,则
,则![]() ,
,
∴![]() . 即
. 即![]() 为奇函数.
为奇函数.
若![]() 则
则![]() 、
、![]() 中至少有一个不为0,
中至少有一个不为0,
当![]() . 则
. 则![]() 故
故![]() .
.
当![]() 时,
时,![]()
![]() 不是奇函数,
不是奇函数,
![]() ,
,![]() , 则
, 则![]() 不是偶函数. 故
不是偶函数. 故![]() 既不是奇函数也不是偶函数.
既不是奇函数也不是偶函数.
综上知:当![]() 时,
时,![]() 为奇函数;
为奇函数;
当![]() 时,
时,![]() 既不是奇函数也不是偶函数.
既不是奇函数也不是偶函数.
(Ⅱ)若![]() 时,
时,![]() 恒成立;
恒成立;
若![]() 时,原不等式可变形为
时,原不等式可变形为![]() . 即
. 即![]() .
.
|
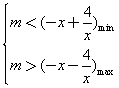
对①式,![]() 在(0,1
在(0,1![]() 上单调递减,
上单调递减,
∴![]() .
.
对②式,设![]() ,则
,则![]() .(因为0<x<1)
.(因为0<x<1)
∴![]() 在
在![]() 上单调递增,
上单调递增,
∴![]() .
.
综上所知:m的范围是(-5,3)。

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目






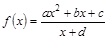 (其中
(其中 是实数常数,
是实数常数, )
) ,函数
,函数 的图像关于点(—1,3)成中心对称,求
的图像关于点(—1,3)成中心对称,求 的值;
的值; ,总有
,总有 ,求
,求 的取值范围;
的取值范围; ,
, ,且对任意
,且对任意 时,不等式
时,不等式 恒成立,求负实数
恒成立,求负实数 的取值范围.
的取值范围.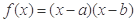 (其中
(其中 )的图象如图(上)所示,则函数
)的图象如图(上)所示,则函数 的图象是( )
的图象是( ) 
