题目内容
12.若f(x)=ex-ae-x为奇函数,则f(x-1)<e-$\frac{1}{e}$的解集为(-∞,2).分析 根据函数奇偶性的性质先求出a的值,结合函数单调性的性质进行求解即可.
解答 解:∵f(x)=ex-ae-x为奇函数,
∴f(0)=0,即f(0)=1-a=0,
则a=1,
即f(x)=ex-e-x,则函数f(x)在(-∞,+∞)上为增函数,
则f(1)=e-$\frac{1}{e}$,
则不等式f(x-1)<e-$\frac{1}{e}$等价为f(x-1)<f(1),
即x-1<1,
解得x<2,
即不等式的解集为(-∞,2),
故答案为:(-∞,2).
点评 本题主要考查不等式的求解,根据函数奇偶性的性质先求出a的值是解决本题的关键.

练习册系列答案
相关题目
2.圆的一条直径为x=2(-2≤y≤0),则此圆的方程是( )
| A. | (x-2)2+(y-1)2=1 | B. | (x-2)2+(y+1)2=1 | C. | (x+2)2+(y-1)2=1 | D. | (x+2)2+(y+1)2=1 |
3.函数y=$\frac{2x}{lnx}$的图象大致为( )
| A. |  | B. | 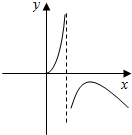 | C. | 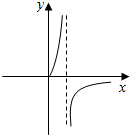 | D. | 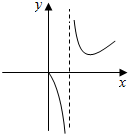 |
17.若实数x,y满足x2+y2-2x+6y+9=0,则|$\sqrt{3}$x+y-$\sqrt{3}$|的最大值、最小值分别为 ( )
| A. | 5、1 | B. | 5、0 | C. | 7、1 | D. | 7、0 |