Question

 (1)已知扇形周长为10，面积是4，求扇形的圆心角；

(2)已知扇形周长为40，当它的半径和圆心角取何值时，才使扇形面积最大？

Answer 1

解析：(1)设圆心角是θ，半径是r，

则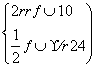⇒或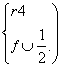

又∵θ∈(0,2π)，∴θ＝8舍去，

∴

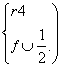
即圆心角为.

(2)设圆心角是θ，半径是r，

则2r＋rθ＝40，

S＝θ·r²＝r(40－2r)＝r(20－r)≤²＝100，

当且仅当r＝20－r，即r＝10时，S_max＝100.

∴当r＝10，θ＝2时，扇形面积最大．

即半径为10，圆心角为2时，扇形面积最大．