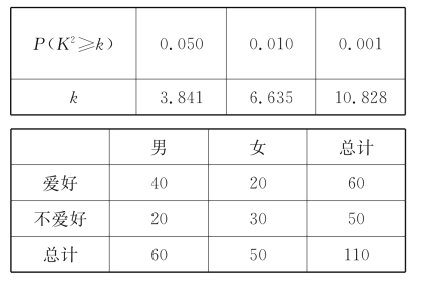
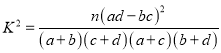题目内容
【题目】某企业为了解下属某部门对本企业职工的服务情况，随机访问50名职工，根据这50名职工对该部门的评分，绘制频率分布直方图(如图)，其中样本数据分组区间为
， 
，…， 
， 
.
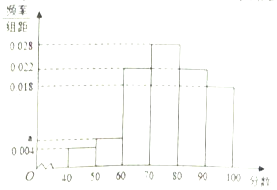
(1)求频率分布图中
的值；
(2)估计该企业的职工对该部门评分不低于80的概率；
(3)从评分在
的受访职工中， 随机抽取2人，求此2人评分都在
的概率.
【答案】(1) 
.(2) 
；(3) 
.
【解析】试题分析：⑴利用频率分布直方图中的信息，所以矩形的面积为
，得到
⑵对该部门评分不低于
的即为
和
，求出频率，估计概率；
⑶求出评分在
的受访职工和评分都在
的人数，随机抽取
人，列举法求出所有可能，利用古典概型公式解答；
解析：(1)因为
，解得
.
(2)由已知的频率分布直方图可知，50名受访职工评分不低于80的频率为
，所以该企业职工对该部门评分不低于80的概率的估计值为
；
(3)受访职工中评分在
的有： 
(人)，记为
；
受访职工评分在
的有： 
(人)，记为
，
从这5名受访职工中随机抽取2人，所有可能的结果共有10种，分别是：
， 
， 
， 
， 
， 
， 
， 
， 
， 
，
又因为所抽取2人的评分都在
的结果只有1种，即
，
故所求的概率为
.
练习册系列答案
相关题目
