题目内容
4.若函数f(x)=$\frac{ax-1}{x-a}$在(-∞,-1)上是增函数,则a的取值范围是a<-1.分析 求出函数的导数,根据函数的单调性得到关于a的不等式组,解出即可.
解答 解:函数f(x)=$\frac{ax-1}{x-a}$,
f′(x)=$\frac{1{-a}^{2}}{{(x-a)}^{2}}$,
若f(x)在(-∞,-1)递增,
则$\left\{\begin{array}{l}{1{-a}^{2}<0}\\{a<-1}\end{array}\right.$,解得:a<-1,
故答案为:a<-1.
点评 本题考查了函数的单调性问题,考查导数的应用,是一道基础题.

练习册系列答案
相关题目
19.直线x+$\sqrt{2}$y-1=0的斜率是( )
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
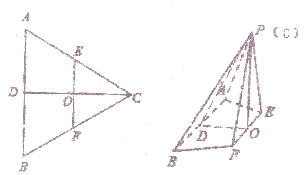 如图,在边长为4的等边三角形ABC中,点D,E,F分别是边AB,AC,BC的中点,DC∩EF=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到如图的四棱锥P-ABFE,且PB=$\sqrt{10}$.
如图,在边长为4的等边三角形ABC中,点D,E,F分别是边AB,AC,BC的中点,DC∩EF=O,沿EF将△CEF翻折到△PEF,连接PA,PB,PD,得到如图的四棱锥P-ABFE,且PB=$\sqrt{10}$. 如图所示,在四面体ABCD中,AD=1,CD=3,AC=2$\sqrt{3}$,cosB=$\frac{{\sqrt{3}}}{3}$.
如图所示,在四面体ABCD中,AD=1,CD=3,AC=2$\sqrt{3}$,cosB=$\frac{{\sqrt{3}}}{3}$.