题目内容
(12分)已知![]() 函数
函数![]() .
.
(Ⅰ)若![]() 在
在![]() 处取得极值,求函数
处取得极值,求函数![]() 的单调区间;
的单调区间;
解析:(Ⅰ)![]()
由![]() 得
得 ![]() …………………………3分
…………………………3分
![]()
当![]() 时,
时,![]() 当
当![]() 时,
时,![]()
故函数![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() . ………………………5分
. ………………………5分
(Ⅱ)由(Ⅰ)![]()
由![]() 得
得 ![]()
当![]() 时,
时,![]() 当
当![]() 时,
时,![]()
![]() 在
在![]() 处取得极大值,
处取得极大值, ![]()
……………………………………7分
(1) 当![]() 时,
时,![]() 函数
函数![]() 在区间为
在区间为![]() 递减 ,
递减 ,
![]()
![]()
(2) 当![]() 时,
时, ![]() ,
,![]()
(3) 当![]() 时,
时,![]() 函数
函数![]() 在区间为
在区间为![]() 递增 ,
递增 ,
![]()


练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知函数 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称 为“一阶比增函数”;若
为“一阶比增函数”;若 在
在 上为增函数,则称
上为增函数,则称 为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为
为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为 ,所有“二阶比增函数”组成的集合记为
,所有“二阶比增函数”组成的集合记为 .
.
(Ⅰ)已知函数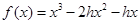 ,若
,若 且
且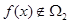 ,求实数
,求实数 的取值范围;
的取值范围;
(Ⅱ)已知 ,
, 且
且 的部分函数值由下表给出,
的部分函数值由下表给出,
|
|
|
|
|
|
|
|
|
|
|
|
求证: ;
;
(Ⅲ)定义集合
请问:是否存在常数 ,使得
,使得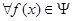 ,
, ,有
,有 成立?若存在,求出
成立?若存在,求出 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.


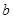
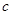




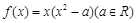 ,
,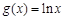 .
.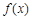 在
在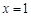 处取得极值,求
处取得极值,求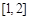 上
上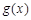 图像的上方(没有公共点),求实数
图像的上方(没有公共点),求实数 的取值范围.
的取值范围. 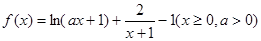 。
。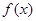 在
在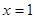 处取得极值,求
处取得极值,求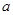 的值;
的值;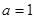 且
且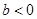 ,函数
,函数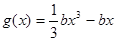 ,若对于
,若对于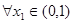 ,总存在
,总存在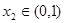 使得
使得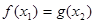 ,求实数
,求实数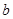 的取值范围。
的取值范围。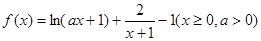 。
。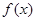 在
在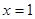 处取得极值,求
处取得极值,求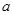 的值;
的值;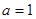 且
且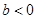 ,函数
,函数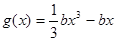 ,若对于
,若对于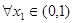 ,总存在
,总存在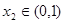 使得
使得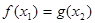 ,求实数
,求实数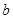 的取值范围。
的取值范围。 ,
, 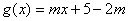 .
.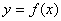 在
在 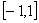 上存在零点,求实数
上存在零点,求实数 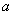 的取值范围;
的取值范围;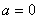 时,若对任意的
时,若对任意的 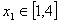 ,总存在
,总存在 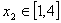 ,使
,使 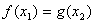 ,求实数
,求实数 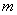 的取值范围.
的取值范围.