题目内容
设α，β是锐角三角形的两内角，则
- A.cosα＞sinβ，cosβ＞sinα
- B.cosα＞sinβ，cosβ＜sinα
- C.cosα＜sinβ，cosβ＜sinα
- D.cosα＜sinβ，cosβ＞sinα
C
分析：由“α、β为锐角三角形的两内角”可得到α+β＞
，转化为 ＞α＞-β＞0，两边再取正弦，可得1＞sinα＞sin（-β）=cosβ＞0，同理可得sinβ＞cosα
解答：∵α、β为锐角三角形的两内角
∴α+β＞
∴＞α＞-β＞0
∴1＞sinα＞sin（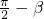
）=cosβ＞0
同理可得sinβ＞cosα
故选C．
点评：题主要考查了三角函数的单调性，属于基础题型．
分析：由“α、β为锐角三角形的两内角”可得到α+β＞
，转化为 ＞α＞-β＞0，两边再取正弦，可得1＞sinα＞sin（-β）=cosβ＞0，同理可得sinβ＞cosα解答：∵α、β为锐角三角形的两内角
∴α+β＞
∴
＞α＞-β＞0∴1＞sinα＞sin（
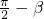）=cosβ＞0同理可得sinβ＞cosα
故选C．
点评：题主要考查了三角函数的单调性，属于基础题型．
练习册系列答案
阅读快车系列答案
相关题目