题目内容
已知双曲线C的对称轴是坐标轴,一条渐近线的方程是![]() ,且该双曲线C经过定点M(3,2)
,且该双曲线C经过定点M(3,2)
(1)求双曲线C的方程;
(2)直线l:ax-y-1=0与双曲线C交于P、Q两点,当实数a为何值时,|PQ|=2![]() ?
?
解:(1)设所求双曲线C的方程为![]() ,将点M的坐标(3,2)代入得
,将点M的坐标(3,2)代入得![]() =1,
=1,
所以双曲线C的方程是![]()
![]()
(2)设P(x1,y1),Q(x2,y2),由 ,
,
得 (1-2a2)x2+4ax-3=0.
若1-2a2=0,即a=±![]() 时,l与C的渐近线平行,l与C只有一个交点,与题意不合,
时,l与C的渐近线平行,l与C只有一个交点,与题意不合,
∴1-2a2≠0,Δ=(4a)2-4(1-2a2)(-3)>0,
∴-![]() <a<
<a<![]() .
.
 (*)
(*)
∴|PQ|=![]() |x1-x2|=2
|x1-x2|=2![]() .
.
∴(x1-x2)2=4,∴(x1+x2)2-4x1x2=4.
∴(-![]() )2-4
)2-4![]() =4.
=4.
∴a=±1∈(-![]() ,
,![]() ).
).
∴所求的实数a的值为a=±1.

练习册系列答案
相关题目
 .
.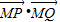 的取值范围.
的取值范围.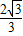 .
.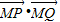 的取值范围.
的取值范围.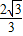 .
. 的取值范围.
的取值范围.