题目内容
已知F1,F2是椭圆 的两个焦点,O为坐标原点,点P(-1,
的两个焦点,O为坐标原点,点P(-1, )在椭圆上,且
)在椭圆上,且 .
.
(1)求椭圆M的方程;
(2)⊙O是以F1F2为直径的圆,直线l:y=kx+m与⊙O相切,并且与椭圆交于不同的两点A,B当 ,且满足
,且满足 时,求弦长|AB|的取值范围.
时,求弦长|AB|的取值范围.
解:(1)依题意,可知PF1⊥F1F2,
∴c=1, ,解得a2=2,b2=1,c2=1
,解得a2=2,b2=1,c2=1
∴椭圆的方程为
(2)直线l:y=kx+m与⊙O:x2+y2=1相切,则m2=k2+1,
由 ,得(1+2k2)x2+4kmx+2m2-2=0,
,得(1+2k2)x2+4kmx+2m2-2=0,
∵直线l与椭圆交于不同的两点A,B
设A(x1,y1),B(x2,y2)
∴
∴y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2= ,
,
∴
∴∴
∴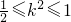 ,
,
∴
设 ,则
,则
∴ ,
,
∴ .
.
分析:(1)根据点P(-1, )在椭圆上,且
)在椭圆上,且 ,可建立方程,从而可求椭圆M的方程;
,可建立方程,从而可求椭圆M的方程;
(2)利用直线l:y=kx+m与⊙O:x2+y2=1相切,可得m2=k2+1,进而将直线与椭圆方程联立,可表示弦长,利用 ,
, ,可确定其范围.
,可确定其范围.
点评:本题以椭圆为载体,考查椭圆的标准方程,考查直线与圆,与椭圆的位置关系,考查弦长的求解,有较强的综合性.
∴c=1,
 ,解得a2=2,b2=1,c2=1
,解得a2=2,b2=1,c2=1∴椭圆的方程为

(2)直线l:y=kx+m与⊙O:x2+y2=1相切,则m2=k2+1,
由
 ,得(1+2k2)x2+4kmx+2m2-2=0,
,得(1+2k2)x2+4kmx+2m2-2=0,∵直线l与椭圆交于不同的两点A,B
设A(x1,y1),B(x2,y2)
∴

∴y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2=
 ,
,∴

∴∴

∴
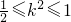 ,
,∴

设
 ,则
,则
∴
 ,
,∴
 .
.分析:(1)根据点P(-1,
 )在椭圆上,且
)在椭圆上,且 ,可建立方程,从而可求椭圆M的方程;
,可建立方程,从而可求椭圆M的方程;(2)利用直线l:y=kx+m与⊙O:x2+y2=1相切,可得m2=k2+1,进而将直线与椭圆方程联立,可表示弦长,利用
 ,
, ,可确定其范围.
,可确定其范围.点评:本题以椭圆为载体,考查椭圆的标准方程,考查直线与圆,与椭圆的位置关系,考查弦长的求解,有较强的综合性.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目