Question

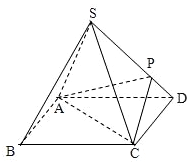如图，四棱锥S-ABCD的底面是正方形，每条侧棱的长都是底面边长的

2

倍，P为侧棱SD上的点．
（Ⅰ）求证：AC⊥SD；
（Ⅱ）若PD：SP=1：3，侧棱SC上是否存在一点E，使得BE∥平面PAC．若存在，求SE：EC的值；若不存在，试说明理由．

Answer 1

分析：（1）由于SD在平面SBD上，证明AC⊥平面SBD，即AC⊥平面内任何线段，即得AC⊥SD．
（2）取SD中点为N，因为PD：SP=1：3，则PN=PD，过N作PC的平行线与SC的交点即为E．在△BDN中知BN∥PO，又由于NE∥PC，
即可得到平面BEN∥平面PAC，使得BE∥平面PAC，进而求得SE：EC的值．

解答：证明：（Ⅰ）连BD，设AC交BD于O，由题意SO⊥AC．
在正方形ABCD中，AC⊥BD，所以AC⊥平面SBD，得AC⊥SD．
（Ⅱ）在棱SC上存在一点E，使BE∥平面PAC
取SD中点为N，因为PD：SP=1：3，则PN=PD，
过N作PC的平行线与SC的交点即为E．连BN．
在△BDN中知BN∥PO，又由于NE∥PC，
故平面BEN∥平面PAC，得BE∥平面PAC，
由于SN：NP=2：1，故SE：EC=2：1．

点评：本题主要考查立体几何中平面与平面平行的性质以及线段垂直平面的性质．