题目内容
椭圆E的中心在坐标原点O,焦点在x轴上,离心率为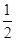 .点P(1,
.点P(1,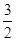 )、A、B在椭圆E上,且
)、A、B在椭圆E上,且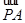 +
+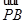 =m
=m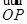 (m∈R).
(m∈R).
(1)求椭圆E的方程及直线AB的斜率;
(2)求证:当△PAB的面积取得最大值时,原点O是△PAB的重心.
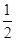 .点P(1,
.点P(1,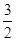 )、A、B在椭圆E上,且
)、A、B在椭圆E上,且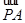 +
+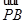 =m
=m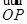 (m∈R).
(m∈R).(1)求椭圆E的方程及直线AB的斜率;
(2)求证:当△PAB的面积取得最大值时,原点O是△PAB的重心.
解:(1)由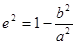 =
=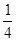 及
及 解得a2=4,b2=3,
解得a2=4,b2=3,
椭圆方程为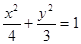 ;…………………………………………………………2分
;…………………………………………………………2分
设A(x1,y1)、B(x2,y2),由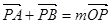 得
得
(x1+x2-2,y1+y2-3)=m(1, ),即
),即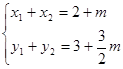
又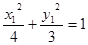 ,
,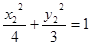 ,两式相减得
,两式相减得
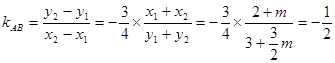 ;………………………6分
;………………………6分
(2)设AB的方程为y=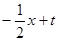 ,代入椭圆方程得:x2-tx+t2-3=0,
,代入椭圆方程得:x2-tx+t2-3=0,
△=3(4-t2),|AB|=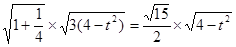 ,
,
点P到直线AB的距离为d=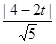 ,
,
S△PAB =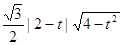 =
=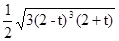 (-2<t<2).……………….10分
(-2<t<2).……………….10分
令f(t) =3(2-t)3(2+t),则f’(t)=-12(2-t)2(t+1),由f’(t)=0得t=-1或2(舍),
当-2<t<-1时,f’(t)>0,当-1<t<2时f’(t)<0,所以当t=-1时,f(t)有最大值81,
即△PAB的面积的最大值是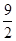 ;
;
根据韦达定理得x1+x2=t=-1,而x1+x2=2+m,所以2+m=-1,得m=-3,
于是x1+x2+1=3+m=0,y1+y2+ =3+
=3+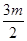 +
+ =0,
=0,
因此△PAB的重心坐标为(0,0).……………………………………………………13分
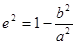 =
=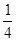 及
及 解得a2=4,b2=3,
解得a2=4,b2=3,椭圆方程为
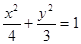 ;…………………………………………………………2分
;…………………………………………………………2分设A(x1,y1)、B(x2,y2),由
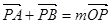 得
得(x1+x2-2,y1+y2-3)=m(1,
 ),即
),即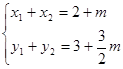
又
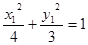 ,
,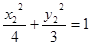 ,两式相减得
,两式相减得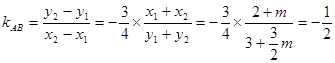 ;………………………6分
;………………………6分(2)设AB的方程为y=
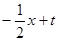 ,代入椭圆方程得:x2-tx+t2-3=0,
,代入椭圆方程得:x2-tx+t2-3=0,△=3(4-t2),|AB|=
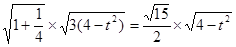 ,
,点P到直线AB的距离为d=
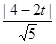 ,
,S△PAB =
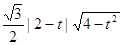 =
=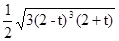 (-2<t<2).……………….10分
(-2<t<2).……………….10分令f(t) =3(2-t)3(2+t),则f’(t)=-12(2-t)2(t+1),由f’(t)=0得t=-1或2(舍),
当-2<t<-1时,f’(t)>0,当-1<t<2时f’(t)<0,所以当t=-1时,f(t)有最大值81,
即△PAB的面积的最大值是
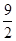 ;
; 根据韦达定理得x1+x2=t=-1,而x1+x2=2+m,所以2+m=-1,得m=-3,
于是x1+x2+1=3+m=0,y1+y2+
 =3+
=3+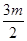 +
+ =0,
=0,因此△PAB的重心坐标为(0,0).……………………………………………………13分
略

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
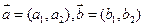 ,定义一种向量积:
,定义一种向量积: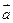
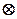
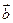 =(a1b1,a2b2).已知点
=(a1b1,a2b2).已知点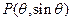 ,
,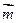 =,
=,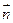 =,点Q在y=f(x)的图象上运动,满足
=,点Q在y=f(x)的图象上运动,满足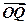 =
=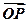 +
+ ,则
,则 的夹角为
的夹角为  中,
中, ,且
,且 ,则边
,则边 的长为
的长为  ,若
,若 ,设
,设 ,则
,则 与
与 轴夹角的余弦值为( )
轴夹角的余弦值为( )



 ,向量b=
,向量b= ,且a⊥b,则
,且a⊥b,则 的值是 。
的值是 。 ,
, ,若
,若 ,则
,则 ( )
( )


 =(-1,1),
=(-1,1), =(1,m)若
=(1,m)若 ,则实数m的值为( )
,则实数m的值为( )