题目内容
(22)已知函数![]() 且存在
且存在![]() 使
使![]()
(I)证明:![]() 是R上的单调增函数;
是R上的单调增函数;
(II)设
其中 ![]()
证明:![]()
(III)证明:![]()
解:(1)∵f′(x)=3x2-2x+![]() =3(x-
=3(x-![]() )2+
)2+![]() >0, ∴f(x)是R上的单调增函数.
>0, ∴f(x)是R上的单调增函数.
(Ⅱ)∵0<x0<![]() , 即 x1<x0<y1. 又f(x)是增函数. ∴f(x1)<f(x0)<f(y1),
, 即 x1<x0<y1. 又f(x)是增函数. ∴f(x1)<f(x0)<f(y1),
即x2<x0<y2, 又 x2=f(x1)=f(0)= ![]() >0=x1,y2=f(y1)=f(
>0=x1,y2=f(y1)=f(![]() )=
)=![]() <
<![]() =y1.
=y1.
综上,x1<x2<x0<y2<y1.
用数学归纳法证明如下:(1)当n=1时,上面已证明成立.
(2)假设当n=k (k≥1)时有 xk<xk+1<x2<yk+1<y2.
当n=k+1时,由f(x)是单调增函数,有f(xk)<f(xk+1)<f(x0)<f(yk+1)<f(yk),
∴xk+1<xk+2<x0<yk+2<yk+1.

练习册系列答案
相关题目
 且
且 (1)求
(1)求 的单调区间;
的单调区间; 与函数
与函数 时有相同的值域,求
时有相同的值域,求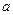 的值;
的值; ,函数
,函数 ,若对于任意
,若对于任意 ,总存在
,总存在 ,使得
,使得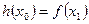 成立,求
成立,求 且存在
且存在 使
使
 是R上的单调增函数;
是R上的单调增函数; 其中
其中 

