题目内容
已知函数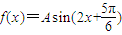 (A>0,x∈R)的最小值为-2.
(A>0,x∈R)的最小值为-2.(1)求f(0);
(2)若函数f(x)的图象向左平移ϕ(ϕ>0)个单位长度,得到的曲线关于y轴对称,求ϕ的最小值.
【答案】分析:(1)由函数的最值求出A,从而求得函数的解析式,进而求得f(0)的值.
(2)函数f(x)的图象变换后得到的图象对应的函数解析式为 ,根据此曲线关于y轴对称,可得
,根据此曲线关于y轴对称,可得 ,由此求得ϕ的最小值.
,由此求得ϕ的最小值.
解答:解:(1)因为函数 (A>0,x∈R)的最小值为-2,
(A>0,x∈R)的最小值为-2,
所以A=2, …(2分),
…(2分),
 .…(4分)
.…(4分)
(2)函数f(x)的图象向左平移ϕ(ϕ>0)个单位长度,可得 .…(6分)
.…(6分)
因为 的图象关于y轴对称,所以
的图象关于y轴对称,所以 .…(8分)
.…(8分)
解得 ,…(10分)
,…(10分)
因为ϕ>0,所以ϕ的最小值为 .…(12分)
.…(12分)
点评:本题主要考查由函数y=Asin(ωx+∅)的部分图象求解析式,函数y=Asin(ωx+∅)的图象变换规律以及对称性,属于中档题.
(2)函数f(x)的图象变换后得到的图象对应的函数解析式为
 ,根据此曲线关于y轴对称,可得
,根据此曲线关于y轴对称,可得 ,由此求得ϕ的最小值.
,由此求得ϕ的最小值.解答:解:(1)因为函数
 (A>0,x∈R)的最小值为-2,
(A>0,x∈R)的最小值为-2,所以A=2,
 …(2分),
…(2分), .…(4分)
.…(4分)(2)函数f(x)的图象向左平移ϕ(ϕ>0)个单位长度,可得
 .…(6分)
.…(6分)因为
 的图象关于y轴对称,所以
的图象关于y轴对称,所以 .…(8分)
.…(8分)解得
 ,…(10分)
,…(10分)因为ϕ>0,所以ϕ的最小值为
 .…(12分)
.…(12分)点评:本题主要考查由函数y=Asin(ωx+∅)的部分图象求解析式,函数y=Asin(ωx+∅)的图象变换规律以及对称性,属于中档题.

练习册系列答案
相关题目
 (A>0,x∈R)的最小值为-2.
(A>0,x∈R)的最小值为-2.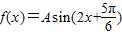 (A>0,x∈R)的最小值为-2.
(A>0,x∈R)的最小值为-2. (a>0,a≠1)的图象恒过定点A,若点A也在函数f(x)=3x+b的图象上,则b= .
(a>0,a≠1)的图象恒过定点A,若点A也在函数f(x)=3x+b的图象上,则b= . 其中a>0.
其中a>0.