题目内容
在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若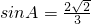 ,a=2,
,a=2, ,则b的值为
,则b的值为
- A.

- B.

- C.

- D.

A
分析:在锐角△ABC中,利用sinA= ,S△ABC=
,S△ABC= ,可求得bc,在利用a=2,由余弦定理可求得b+c,解方程组可求得b的值.
,可求得bc,在利用a=2,由余弦定理可求得b+c,解方程组可求得b的值.
解答:∵在锐角△ABC中,sinA= ,S△ABC=
,S△ABC= ,
,
∴ bcsinA=
bcsinA= bc
bc =
= ,
,
∴bc=3,①
又a=2,A是锐角,
∴cosA=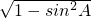 =
= ,
,
∴由余弦定理得:a2=b2+c2-2bccosA,
即(b+c)2=a2+2bc(1+cosA)=4+6(1+ )=12,
)=12,
∴b+c=2 ②
②
由①②得: ,
,
解得b=c= .
.
故选A.
点评:本题考查正弦定理与余弦定理的应用,考查方程思想与运算能力,属于中档题.
分析:在锐角△ABC中,利用sinA=
 ,S△ABC=
,S△ABC= ,可求得bc,在利用a=2,由余弦定理可求得b+c,解方程组可求得b的值.
,可求得bc,在利用a=2,由余弦定理可求得b+c,解方程组可求得b的值.解答:∵在锐角△ABC中,sinA=
 ,S△ABC=
,S△ABC= ,
,∴
 bcsinA=
bcsinA= bc
bc =
= ,
,∴bc=3,①
又a=2,A是锐角,
∴cosA=
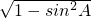 =
= ,
,∴由余弦定理得:a2=b2+c2-2bccosA,
即(b+c)2=a2+2bc(1+cosA)=4+6(1+
 )=12,
)=12,∴b+c=2
 ②
②由①②得:
 ,
,解得b=c=
 .
.故选A.
点评:本题考查正弦定理与余弦定理的应用,考查方程思想与运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目