题目内容
已知
是定义在
上的奇函数，且当
时，
．
（Ⅰ）求的解析式；
（Ⅱ）直接写出的单调区间（不需给出演算步骤）；
（Ⅲ）求不等式
解集．
解：（Ⅰ）当
时，
；
当
时，则
，
，则
综上：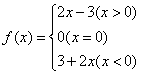
（Ⅱ）递增区间：
，
（Ⅲ）当
时，
，即
当时，
，即
当时，
，恒成立
综上，所求解集为：
练习册系列答案
相关题目
题目内容
已知是定义在上的奇函数，且当时，．
（Ⅰ）求的解析式；
（Ⅱ）直接写出的单调区间（不需给出演算步骤）；
（Ⅲ）求不等式解集．
解：（Ⅰ）当时，；
当时，则，，则
综上：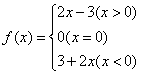
（Ⅱ）递增区间：，
（Ⅲ）当时，，即
当时，，即
当时，，恒成立
综上，所求解集为：
是定义在
上的奇函数，且
，
的解析式；
.
是定义在R上的奇函数，且
，在[0，2]上
，则
；[来源:Z§xx§k.Com]
且
；
在[-8，8]内恰有四个不同的根
，则
；
是定义在
上的不恒为零的函数，且对于任意实数
都有
, 则