题目内容
已知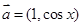 ,
,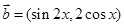 ,且
,且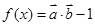
(1)求函数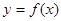
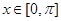 的单调增区间;
的单调增区间;
(2)三角形ABC中,边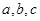 分别为角
分别为角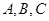 的对边,若
的对边,若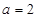 ,B=
,B=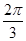 ,且
,且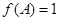 ,
求三角形ABC的边
,
求三角形ABC的边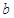 的值.
的值.
【答案】
(1)单调增区间为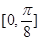 和
和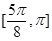 ;(2)
;(2)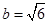 .
.
【解析】
试题分析:(1)首先由向量的数量积及坐标运算得函数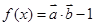 的解析式,利用正弦函数的单调区间即可求得该函数的单调区间;(2)注意直线
的解析式,利用正弦函数的单调区间即可求得该函数的单调区间;(2)注意直线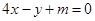 的斜率为4,那么要证明无论
的斜率为4,那么要证明无论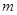 为何值,直线
为何值,直线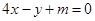 与函数
与函数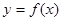 的图象不相切,就只需通过求导说明函数的导数值不可能等于4即可.
的图象不相切,就只需通过求导说明函数的导数值不可能等于4即可.
(2)由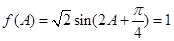 可求得角A.这样本题就是典型的已知两角及一边的解三角形问题,用正弦定理即可求得
可求得角A.这样本题就是典型的已知两角及一边的解三角形问题,用正弦定理即可求得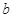 的值.
的值.
试题解析:(1)∵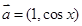 ,
,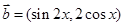 ,且
,且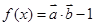
∴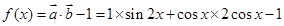 1分
1分
=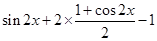 =
=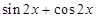
=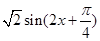 3分
3分
令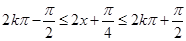 ,解之得
,解之得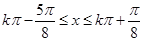 4分
4分
又∵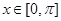 ∴
∴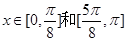
故函数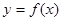
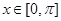 的单调增区间为
的单调增区间为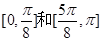 6分
6分
(2)由①问可知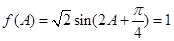
∴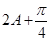 =
= 或
或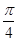 ,即
,即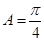 或
或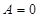 8分
8分
∵A是三角形ABC的内角 ∴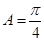
又∵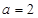 ,B=
,B=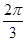 ∴由正弦定理有
∴由正弦定理有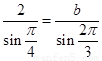 ,即有
,即有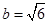 12分
12分
考点:1、向量的数量积及坐标运算;2、三角变换及三角函数的单调区间;3、解三角形.

练习册系列答案
相关题目
 ,
, ,且
,且

 的单调增区间;
的单调增区间; 为何值,直线
为何值,直线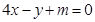 与函数
与函数 ,且
,且
 的解析式和它的最小正周期;
的解析式和它的最小正周期; 的值域。
的值域。