题目内容
(本小题12分)已知函数
(1)若函数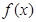 的值域为
的值域为 ,求实数
,求实数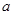 的取值范围;
的取值范围;
(2)当 时,函数
时,函数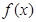 恒有意义,求实数
恒有意义,求实数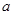 的取值范围。
的取值范围。
【答案】
(1)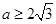 ;(2)
;(2)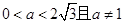
【解析】
试题分析:(1)对数函数的值域为R,意味着真数可以取遍一切正实数,故内层二次函数应与x轴有交点,即△≥0,解得a的范围;
(2)函数f(x)恒有意义,即真数大于零恒成立,利用参变分离法解决此恒成立问题即可得a的取值范围
解:(1)令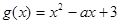 ,由题设知
,由题设知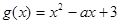 需取遍
需取遍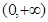 内任意值,所以
内任意值,所以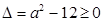 解得
解得 ,由于
,由于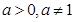 所以
所以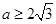
(2)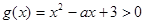 对一切
对一切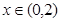 恒成立且
恒成立且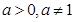
即 对一切
对一切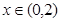 恒成立 ,
恒成立 ,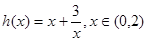 ,当
,当 时,
时,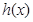 取得最小值为
取得最小值为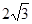 ,所以
,所以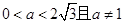
考点:本题主要考查了对数复合函数的定义域和值域,已知函数的值域求参数的范围,已知函数的定义域求参数范围,转化化归的思想方法。
点评:解决该试题的关键是能将不等式的恒成立问题,转换为函数的最值问题,运用分离参数 三四箱来得到参数a的取值范围。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 中,
中, 。
。 中,
中, ,求数列
,求数列 项和
项和 .
. 轴上的抛物线与直线
轴上的抛物线与直线 交于P、Q两点,|PQ|=
交于P、Q两点,|PQ|= ,求抛物线的方程
,求抛物线的方程 ;
; 过
过 且与圆C相切,求直线
且与圆C相切,求直线 ,使直线
,使直线
 处的切线方程。
处的切线方程。