题目内容
(本小题满分12分)设函数 ,直线
,直线 与函数
与函数 图像相邻两交点的距离为
图像相邻两交点的距离为 .
.
(1)求 的值;
的值;
(2)在 中,角
中,角 所对的边分别是
所对的边分别是 ,若点
,若点 是函数
是函数 图像的一个对称中心,且
图像的一个对称中心,且 =3,求
=3,求 面积的最大值.
面积的最大值.
(1) ;(2)
;(2)
【解析】
试题分析:(1)用余弦二倍角公式和化一公式将函数 化简可得
化简可得 .因为函数
.因为函数 的最大值为
的最大值为 ,所以直线
,所以直线 与函数
与函数 图像相邻两交点的距离为一个周期,即
图像相邻两交点的距离为一个周期,即 .根据周期公式
.根据周期公式 可求得
可求得 .(2)点
.(2)点 是函数
是函数 图像的一个对称中心,可得
图像的一个对称中心,可得 从而可求得
从而可求得 .根据余弦定理可求得
.根据余弦定理可求得 ,再根据基本不等式可求得
,再根据基本不等式可求得 的范围.再根据三角形面积公式
的范围.再根据三角形面积公式 可求得面积的最大值.
可求得面积的最大值.
试题解析:【解析】
(1)

 的最大值为
的最大值为 ,
, 的最小正周期为
的最小正周期为 ,
,  6分
6分
(2)由(1)知 ,
,
因为点 是函数
是函数 图像的一个对称中心
图像的一个对称中心
 , 8分
, 8分
 ,
, ,
,
故 ,
, 面积的最大值为
面积的最大值为 . 12分
. 12分
考点:1三角函数化简,周期;2余弦定理;3基本不等式.

练习册系列答案
相关题目
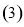 班共有学生
班共有学生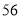 人,现根据座号,用系统抽样的方法,抽取一个容量为
人,现根据座号,用系统抽样的方法,抽取一个容量为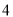 的样本.已知
的样本.已知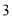 号、
号、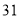 号、
号、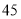 号同学在样本中,那么样本中还有一个同学的座号是( )
号同学在样本中,那么样本中还有一个同学的座号是( )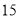 B.
B.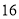 C.
C.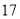 D.
D.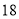
 中,内角A,B,C所对的边长分别为
中,内角A,B,C所对的边长分别为

 B.
B. C.
C. D.
D.
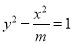 的离心率
的离心率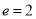 ,则以双曲线的两条渐近线与抛物线
,则以双曲线的两条渐近线与抛物线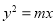 的交点为顶点的三角形的面积为
的交点为顶点的三角形的面积为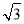 B.
B. C.
C.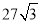 D.
D.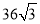
 的焦点坐标为
的焦点坐标为 B.
B. C.
C. D.
D.
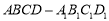 中分离出来的.如果用图示中这样一个装置来盛水,那么最多能盛
中分离出来的.如果用图示中这样一个装置来盛水,那么最多能盛 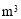 体积的水.
体积的水.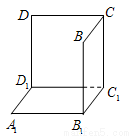

 的单调递增区间为 .
的单调递增区间为 . 的定义域为
的定义域为 ,则实数
,则实数 的取值范围为 .
的取值范围为 .