题目内容
设定义在(0,+∞)上的函数f(x)满足;对任意a,b∈(0,+∞),都有f(b)=f(a)-f(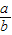 ),且当x>1时,f(x)>0.
),且当x>1时,f(x)>0.(1)求f(1)的值;
(2)判断并证明函数f(x)的单调性;
(3)如果f(3)=1,解不等式f(x)-f(
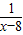 )>2.
)>2.
【答案】分析:(1)令a=b=1,得f(1)=f(1)-f(1)=0,即可求出f(1);
(2)设x1,x2∈(0,+∞),设x1<x2,,由已知得出f(x2)-f(x1)=f(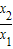 ),且能得出f(
),且能得出f(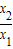 )>0,确定出f(x1)<f(x2)后即可判断出函数f(x)在R上单调性.
)>0,确定出f(x1)<f(x2)后即可判断出函数f(x)在R上单调性.
(3)由(2),不等式化为f(x(x-8))>f(9),即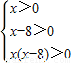 ,利用解不等式的方法得出x的取值范围.
,利用解不等式的方法得出x的取值范围.
解答:解:(1)取a=b=1,得f(1)=f(1)-f(1)=0,所以f(1)=0.
(2)函数在(0,+∞)上是单调增函数.
任取x1,x2∈(0,+∞),设x1<x2,则f(x2)-f(x1)=f(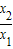 ),因为0<x1<x2,所以
),因为0<x1<x2,所以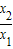 >1,又当x>1时,有f(x)>0,所以f(x2)-f(x1)=f(
>1,又当x>1时,有f(x)>0,所以f(x2)-f(x1)=f(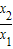 )>0,即f(x2)>f(x1).所以f(x)在(0,+∞)上是单调增函数.
)>0,即f(x2)>f(x1).所以f(x)在(0,+∞)上是单调增函数.
(3)若f(3)=1,则2=1+1=f(3)+f(3)=f(9),f(x)-f(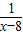 )=f(x(x-8)),则不等式f(x)-f(
)=f(x(x-8)),则不等式f(x)-f(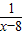 )>2可以化为f(x(x-8))>f(9),即
)>2可以化为f(x(x-8))>f(9),即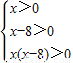 ,解得x>9.即不等式的解集为(9,+∞).
,解得x>9.即不等式的解集为(9,+∞).
点评:本题考查抽象函数求函数值、单调性的判定、及单调性的应用,考查转化、分离参数的思想方法.牢牢把握所给的关系式,对式子中的字母准确灵活的赋值,变形构造是解决抽象函数问题常用的思路.
(2)设x1,x2∈(0,+∞),设x1<x2,,由已知得出f(x2)-f(x1)=f(
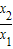 ),且能得出f(
),且能得出f(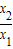 )>0,确定出f(x1)<f(x2)后即可判断出函数f(x)在R上单调性.
)>0,确定出f(x1)<f(x2)后即可判断出函数f(x)在R上单调性.(3)由(2),不等式化为f(x(x-8))>f(9),即
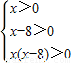 ,利用解不等式的方法得出x的取值范围.
,利用解不等式的方法得出x的取值范围.解答:解:(1)取a=b=1,得f(1)=f(1)-f(1)=0,所以f(1)=0.
(2)函数在(0,+∞)上是单调增函数.
任取x1,x2∈(0,+∞),设x1<x2,则f(x2)-f(x1)=f(
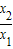 ),因为0<x1<x2,所以
),因为0<x1<x2,所以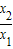 >1,又当x>1时,有f(x)>0,所以f(x2)-f(x1)=f(
>1,又当x>1时,有f(x)>0,所以f(x2)-f(x1)=f(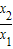 )>0,即f(x2)>f(x1).所以f(x)在(0,+∞)上是单调增函数.
)>0,即f(x2)>f(x1).所以f(x)在(0,+∞)上是单调增函数.(3)若f(3)=1,则2=1+1=f(3)+f(3)=f(9),f(x)-f(
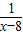 )=f(x(x-8)),则不等式f(x)-f(
)=f(x(x-8)),则不等式f(x)-f(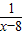 )>2可以化为f(x(x-8))>f(9),即
)>2可以化为f(x(x-8))>f(9),即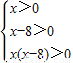 ,解得x>9.即不等式的解集为(9,+∞).
,解得x>9.即不等式的解集为(9,+∞).点评:本题考查抽象函数求函数值、单调性的判定、及单调性的应用,考查转化、分离参数的思想方法.牢牢把握所给的关系式,对式子中的字母准确灵活的赋值,变形构造是解决抽象函数问题常用的思路.

练习册系列答案
相关题目