题目内容
19.函数$f(x)=\frac{1}{3}{x^3}-\frac{a}{2}{x^2}+bx+c$,曲线y=f(x)在点(0,f(0))处的切线方程为y=1.(1)求b,c的值;
(2)设函数g(x)=f(x)+2x,g(x)在R上为单调递增,求实数a的取值范围.
分析 (1)求函数的导数,利用导数的几何意义建立方程即可求b,c的值;
(2)求函数的导数,利用g(x)在R上为单调递增,转化为g′(x)≥0恒成立,进行求解即可.
解答 解:(1)f(0)=c,
函数的导数f′(x)=x2-ax+b,
则函数在点(0,f(0))处的切线斜率k=f′(0)=b,
即切线方程为y-c=bx,即y=bx+c,
∵曲线y=f(x)在点(0,f(0))处的切线方程为y=1,
∴b=0,c=0
(2)∵b=0,c=0
∴f(x)=$\frac{1}{3}$x3-$\frac{a}{2}$x2,f′(x)=x2-ax,
则g(x)=f(x)+2x在R上为单调递增,
则g′(x)=f′(x)+2=x2-ax+2≥0恒成立,
即判别式△=a-8≤0,即a≤8,
即实数a的取值范围是a≤8.
点评 本题主要考查导数的应用,根据导数的几何意义以及函数单调性和导数之间的关系进行转化是解决本题的关键.

练习册系列答案
相关题目
9.6本相同的数学书和3本不相同的语文书分给9个人,每人1本,共有不同分法( )
| A. | C${\;}_{9}^{3}$ | B. | A${\;}_{9}^{3}$ | C. | A${\;}_{9}^{6}$ | D. | A${\;}_{9}^{3}$•A${\;}_{3}^{3}$ |
7.已知某空间几何体的三视图如图所示,则该几何体的体积为( )
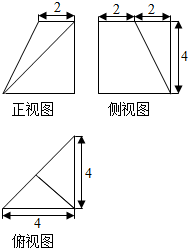

| A. | $\frac{16}{3}$ | B. | $\frac{80}{3}$ | C. | $\frac{40}{3}$ | D. | 40 |
8.已知y=f(x)是奇函数,且f(4)=5,那么f(4)+f(-4)的值为( )
| A. | -5 | B. | 0 | C. | 10 | D. | -10 |