题目内容
在三棱锥A—BCD中,侧棱AB、AC、AD两两垂直,△ABC、△ACD、△ADB的面积分别为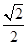 、
、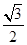 、
、 ,则三棱锥A—BCD的外接球的体积为 ( )
,则三棱锥A—BCD的外接球的体积为 ( )
A.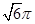 B.2
B.2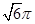 C.3
C.3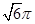 D.4
D.4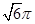
A
解析试题分析:因为,在三棱锥A—BCD中,侧棱AB、AC、AD两两垂直,△ABC、△ACD、△ADB的面积分别为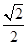 、
、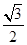 、
、 ,设侧棱AB、AC、AD分别为a,b,c,则
,设侧棱AB、AC、AD分别为a,b,c,则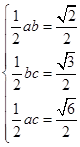 ,解得
,解得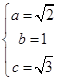 ,将此三棱锥补成长方体,则体对角线即为外接球的直径
,将此三棱锥补成长方体,则体对角线即为外接球的直径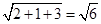 ,所以,三棱锥A—BCD的外接球的体积为
,所以,三棱锥A—BCD的外接球的体积为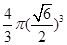 =
=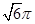 ,选A。
,选A。
考点:本题主要考查三棱锥的几何特征,球的体积公式。
点评:中档题,从已知出发确定侧棱的长,补成长方体是进一步解题的关键。

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
已知在△ABC中,sinA∶sinB∶sinC=3∶5∶7,那么这个三角形的最大角是 ( )
| A.135° | B.90° | C.120° | D.150 |
在 中,内角
中,内角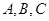 所对的边分别为
所对的边分别为 。已知
。已知 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
 中
中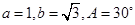 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
在 中,已知
中,已知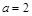 ,
, ,
, ,则
,则 的面积是( ).
的面积是( ).
A. | B. | C. | D. |
△ABC中,a=2bcosC,则此三角形一定是( )
| A.等腰三角形 | B.直角三角形 |
| C.等腰直角三角形 | D.等腰或直角三角形 |
在△ 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 ,则角
,则角 的值为( )
的值为( )
A. | B. | C. | D. |
在 中,
中, 则
则 ( )
( )
A. | B. | C. | D. |
 (a,b, c分别为角A、B、C的对边),则△ABC的形状为
(a,b, c分别为角A、B、C的对边),则△ABC的形状为