题目内容
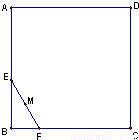
 如图,线段EF的长度为1,端点E,F在边长不小于1的正方形ABCD的四边上滑动,当E,F沿正方形的四边滑动一周时,EF的中点M所形成的轨迹为G,若G的周长为l,其围成的面积为S,则l-S的最大值为
如图,线段EF的长度为1,端点E,F在边长不小于1的正方形ABCD的四边上滑动,当E,F沿正方形的四边滑动一周时,EF的中点M所形成的轨迹为G,若G的周长为l,其围成的面积为S,则l-S的最大值为| 5 |
| 4 |
| 5 |
| 4 |
分析:确定轨迹为G是四个角处的四个直角扇形与正方形的四条边上的四条线段组成,然后根据圆的周长公式、面积公式可得l-S的表达式,利用配方法可求最大值.
解答:解:在正方形的每个角上,G是半径为
的
圆,周长为:2π×0.5=π
设正方形边长为a(a>1),则l=π+4a-4,S=a2-
∴l-S=-a2+4a-4+
π=-(a-2)2+
π
∴当a=2时,l-S的最大值为
π
故答案为:
π
| 1 |
| 2 |
| 1 |
| 4 |
设正方形边长为a(a>1),则l=π+4a-4,S=a2-
| π |
| 4 |
∴l-S=-a2+4a-4+
| 5 |
| 4 |
| 5 |
| 4 |
∴当a=2时,l-S的最大值为
| 5 |
| 4 |
故答案为:
| 5 |
| 4 |
点评:本题考查轨迹的确定,考查函数模型的构建,考查函数的最值,确定轨迹是关键.

练习册系列答案
相关题目
 如图,正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于
如图,正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于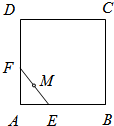 如图,设线段EF的长度为1,端点E、F在边长为2的正方形ABCD的四边上滑动.当E、F沿着正方形的四边滑动一周时,EF的中点M所形成的轨迹为G,若G围成的面积为S,则S=
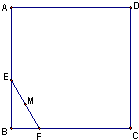
如图,设线段EF的长度为1,端点E、F在边长为2的正方形ABCD的四边上滑动.当E、F沿着正方形的四边滑动一周时,EF的中点M所形成的轨迹为G,若G围成的面积为S,则S= 如图,线段EF的长度为1,端点E,F在边长不小于1的正方形ABCD的四边上滑动,当E,F沿正方形的四边滑动一周时,EF的中点M所形成的轨迹为G,若G的周长为l,其围成的面积为S,则l-S的最大值为________.
如图,线段EF的长度为1,端点E,F在边长不小于1的正方形ABCD的四边上滑动,当E,F沿正方形的四边滑动一周时,EF的中点M所形成的轨迹为G,若G的周长为l,其围成的面积为S,则l-S的最大值为________.