题目内容
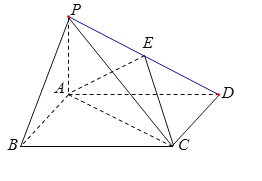
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() 平面
平面![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)证明:![]() ∥平面
∥平面![]() .
.
(2)设二面角![]() 为
为![]() ,
,![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析(2)![]()
【解析】
(1)连结![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() . 根据四边形
. 根据四边形![]() 为矩形,所以
为矩形,所以![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 的中点,利用三角形的中位线可得
的中点,利用三角形的中位线可得![]() ∥
∥![]() ,再利用线面平行的判定定理证明.
,再利用线面平行的判定定理证明.
(2) 根据![]() 平面
平面![]() ,四边形
,四边形![]() 为矩形,建立空间直角坐标系
为矩形,建立空间直角坐标系![]() .设
.设![]() ,再求得平面DAE, 平面CAE的法向量,根据二面角
,再求得平面DAE, 平面CAE的法向量,根据二面角![]() 为
为![]() ,利用
,利用![]() ,解得
,解得![]() .,然后利用锥体体积公式求解.
.,然后利用锥体体积公式求解.
(1)连结![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() .
.
因为四边形![]() 为矩形,所以
为矩形,所以![]() 为
为![]() 的中点,
的中点,
又![]() 为
为![]() 的中点,所以
的中点,所以![]() ∥
∥![]() ,
,
且![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]() .
.
(2) 因为![]() 平面
平面![]() ,四边形
,四边形![]() 为矩形,所以
为矩形,所以![]() 两两垂直,
两两垂直,
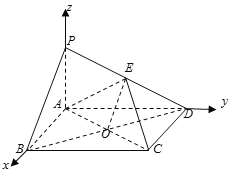
以![]() 为坐标原点,
为坐标原点,![]() 的方向为
的方向为![]() 轴的正方向,
轴的正方向,![]() 的方向为
的方向为![]() 轴的正方向,
轴的正方向,![]() 的方向为
的方向为![]() 轴的正方向,
轴的正方向,![]() 为单位长,建立空间直角坐标系
为单位长,建立空间直角坐标系![]() .
.
设![]() ,则
,则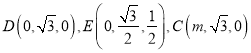 ,
,
所以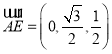 ,
,![]()
设![]() 为平面
为平面![]() 的法向量,则
的法向量,则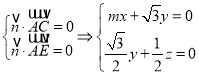 ,
,
可取![]() ,
,
又![]() 为平面
为平面![]() 的一个法向量,由题设知
的一个法向量,由题设知![]()
即![]() ,解得
,解得![]() .
.
因为![]() 为
为![]() 的中点,设
的中点,设![]() 为
为![]() 的中点,
的中点,
则![]() ∥
∥![]() ,且
,且![]() ,
,![]() ⊥面
⊥面![]() ,
,
故有三棱锥![]() 的高为
的高为![]() ,
,
三棱锥![]() 的体积
的体积![]()
所以三棱锥![]() 的体积为
的体积为![]() .
.

练习册系列答案
相关题目
【题目】支付宝和微信支付已经成为现如今最流行的电子支付方式,某市通过随机询问100名居民(男女居民各50名)喜欢支付宝支付还是微信支付,得到如下的![]() 列联表:
列联表:
支付宝支付 | 微信支付 | |
男 | 40 | 10 |
女 | 25 | 25 |
附表及公式: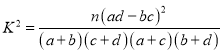 ,
,![]() .
.
P( | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
则下面结论正确的是( )
A.有![]() 以上的把握认为“支付方式与性别有关”
以上的把握认为“支付方式与性别有关”
B.在犯错误的概率超过![]() 的前提下,认为“支付方式与性别有关”
的前提下,认为“支付方式与性别有关”
C.在犯错误的概率不超过![]() 的前提下,认为“支付方式与性别有关”
的前提下,认为“支付方式与性别有关”
D.有![]() 以上的把握认为“支付方式与性别无关”
以上的把握认为“支付方式与性别无关”