Question

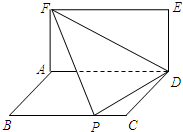矩形ABCD与矩形ADEF所在的平面互相垂直，将△DEF沿FD翻折，翻折后的点E恰与BC上的点P重合．设AB=1，FA=x（x＞1），AD=y，则当x=

 

时，y有最小值．

Answer 1

分析：由已知中矩形ABCD与矩形ADEF所在的平面互相垂直，将△DEF沿FD翻折，翻折后的点E恰与BC上的点P重合．设AB=1，FA=x（x＞1），AD=y，我们利用勾股定理分别求出BP，PC，根据BC=BP+PC，可以得到 x，y的关系式，利用换元法结合二次函数的性质，可得答案．

解答：解：∵形ABCD与矩形ADEF所在的平面互相垂直，
AB=1，FA=x（x＞1），AD=y，
∴FE=FP=AD=BC=y，AB=DC=1，FA=DE=DP=x
在Rt△DCP中，PC=

x2-1

在Rt△FAP中，AP=

y2-x2

在Rt△ABP中，BP=

y2-x2-1

∵BC=BP+PC=

y2-x2-1

+

x2-1

=y
整理得y²=

x4

x2-1

=

1

1 X2 - 1 x4

，令t=

1

x2

则y²=

1

-t2+t

，
则当t=

1

2

，即x=

2

时，y取最小值．
故答案为：

2

点评：本题考查的知识点是空间两点之间的距离计算，由于本题是几何与代数知识的综合应用，运算量比较大，而且得到的x，y的关系比较复杂，因此要用换元法，简单表达式．