题目内容
已知函数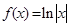
 ,函数
,函数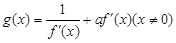
⑴当 时,求函数
时,求函数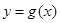 的表达式;
的表达式;
⑵若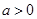 ,函数
,函数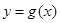 在
在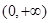 上的最小值是2 ,求
上的最小值是2 ,求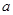 的值;
的值;
(3)⑵的条件下,求直线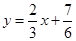 与函数
与函数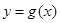 的图象所围成图形的面积.
的图象所围成图形的面积.
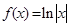
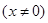 ,函数
,函数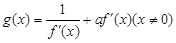
⑴当
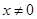 时,求函数
时,求函数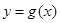 的表达式;
的表达式;⑵若
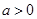 ,函数
,函数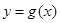 在
在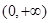 上的最小值是2 ,求
上的最小值是2 ,求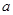 的值;
的值;(3)⑵的条件下,求直线
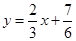 与函数
与函数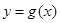 的图象所围成图形的面积.
的图象所围成图形的面积.⑴当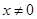 时,函数
时,函数
⑵
(3)
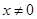 时,函数
时,函数
⑵

(3)

试题分析:(1)对x的取值分类讨论,化简绝对值,求出
 得到
得到 和
和 导函数相等,代入到
导函数相等,代入到 中得到即可;
中得到即可;(2)根据基本不等式得到
 的最小值即可求出
的最小值即可求出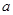 ;
;(3)根据(2)知
 先联立直线与函数解析式求出交点,利用定积分求直线和函数图象围成面积的方法求出即可.
先联立直线与函数解析式求出交点,利用定积分求直线和函数图象围成面积的方法求出即可.⑴∵
 ,
,∴当
 时,
时, ; 当
; 当 时,
时,
∴当
 时,
时, ; 当
; 当 时,
时, .
.∴当
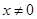 时,函数
时,函数 .
.⑵∵由⑴知当
 时,
时, ,
,∴当
 时,
时,  当且仅当
当且仅当 时取等号.
时取等号.∴函数
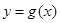 在
在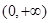 上的最小值是
上的最小值是 ,∴依题意得
,∴依题意得 ∴
∴ .
.⑶由
 解得
解得
∴直线
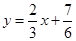 与函数
与函数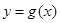 的图象所围成图形的面积
的图象所围成图形的面积 =
=

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
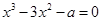 有三个不同的实数解,则a的取值范围是__________.
有三个不同的实数解,则a的取值范围是__________.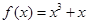 ,
,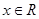 .若当
.若当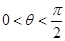 时,不等式
时,不等式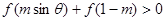 恒成立,则实数
恒成立,则实数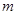 的取值范围是( )
的取值范围是( )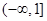
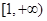
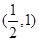
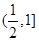
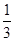 x3-
x3-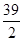 x2-40x(x>0),为使耗电量最小,则速度应定为________.
x2-40x(x>0),为使耗电量最小,则速度应定为________.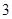 元,并且每件产品需向总公司交
元,并且每件产品需向总公司交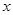 元(
元(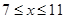 )时,一年的销售量为
)时,一年的销售量为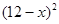 万件.
万件.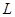 (万元)与每件产品的售价
(万元)与每件产品的售价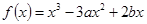 在x=1处有极小值-1,
在x=1处有极小值-1,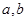 的值; (2)求出
的值; (2)求出 的单调区间.
的单调区间.