题目内容
以F1(0 ,-1),F2(0 ,1)为焦点的椭圆C过点P(![]() ,1).
,1).
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点S(![]() ,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T ? 若存在,求出点T的坐标;若不存在,请说明理由.
,0)的动直线l交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得无论l如何转动,以AB为直径的圆恒过点T ? 若存在,求出点T的坐标;若不存在,请说明理由.
解: (Ⅰ)设椭圆方程为![]() (a>b>0),由已知c =1,
(a>b>0),由已知c =1,
又2a= 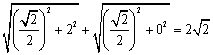 . 则a=
. 则a=![]() ,b2=a2-c2=1,
,b2=a2-c2=1,
椭圆C的方程是![]() + x2 =1. 。。。。。。。。。。。。。。。4分
+ x2 =1. 。。。。。。。。。。。。。。。4分
(Ⅱ)若直线l与x轴重合,则以AB为直径的圆是x2+y2=1,
若直线l垂直于x轴,则以AB为直径的圆是(x+![]() )2+y2=
)2+y2=![]() .
.
由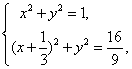 解得
解得![]() 即两圆相切于点(1,0).因此所求的点T如果存在,只能是(1,0). 事实上,点T(1,0)就是所求的点.证明如下: 。。6分
即两圆相切于点(1,0).因此所求的点T如果存在,只能是(1,0). 事实上,点T(1,0)就是所求的点.证明如下: 。。6分
当直线l垂直于x轴时,以AB为直径的圆过点T(1,0).若直线l不垂直于x轴,可设直线l:y=k(x+![]() ).由
).由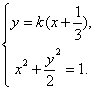 即(k2+2)x2+
即(k2+2)x2+![]() k2x+
k2x+![]() k2-2=0.记点A(x1,y1),B(x2,y2),则
k2-2=0.记点A(x1,y1),B(x2,y2),则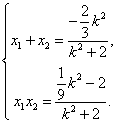 又因为
又因为![]() =(x11, y1),
=(x11, y1), ![]() =(x21, y2),
=(x21, y2),![]() ·
·![]() =(x11)(x21)+y1y2=(x11)(x21)+k2(x1+
=(x11)(x21)+y1y2=(x11)(x21)+k2(x1+![]() )(x2+
)(x2+![]() )=(k2+1)x1x2+(
)=(k2+1)x1x2+(![]() k21)(x1+x2)+
k21)(x1+x2)+![]() k2+1=(k2+1)
k2+1=(k2+1) 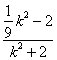 +(
+(![]() k21)
k21) ![]() +
+ ![]() +1=0,则TA⊥TB,故以AB为直径的圆恒过点T(1,0).所以在坐标平面上存在一个定点T(1,0)满足条件. 。。。。。。。。。。。。。。。。12分
+1=0,则TA⊥TB,故以AB为直径的圆恒过点T(1,0).所以在坐标平面上存在一个定点T(1,0)满足条件. 。。。。。。。。。。。。。。。。12分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目