题目内容
椭圆
+y2=1的离心率为( )
| x2 |
| 4 |
分析:根据椭圆的标准方程后,找出a与b的值,然后根据a2=b2+c2求出c的值,利用离心率公式e=
,把a与c的值代入即可求出值.
| c |
| a |
解答:解:由椭圆的标准方程
+y2=1,得到a=2,b=1,
则c=
=
,所以椭圆的离心率e=
=
.
故选A.
| x2 |
| 4 |
则c=
| 4-1 |
| 3 |
| c |
| a |
| ||
| 2 |
故选A.
点评:此题考查学生掌握椭圆的离心率的求法,灵活运用椭圆的简单性质化简求值,是一道基础题.

练习册系列答案
相关题目
椭圆
+y2=1的两个焦点为F1、F2,过F1作垂直于x轴的直线与椭圆相交,一个交点为P,则P到F2的距离为( )
| x2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、4 |
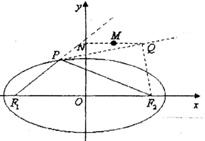 如图,已知椭圆
如图,已知椭圆