题目内容
已知椭圆C1: +
+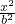 =1(a>b>0),的右焦点为F,上顶点为A,P为C1上任一点,圆心在y轴上的圆C2与斜率为-1的直线l切于点B(-
=1(a>b>0),的右焦点为F,上顶点为A,P为C1上任一点,圆心在y轴上的圆C2与斜率为-1的直线l切于点B(- ,3-
,3- ),且AF∥l.
),且AF∥l.
(1)求圆的方程及椭圆的离心率.
(2)过P作圆C2的切线PE,PG,若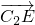
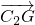 的最小值为-
的最小值为-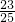 ,求椭圆的方程.
,求椭圆的方程.
解:(1)由圆心在y轴上的圆C2与斜率为1的直线l切于点B(-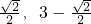 ),所以圆心在过B且垂直于l的直线y=x+3上,又圆心在y轴上,则圆心C2(0,3),
),所以圆心在过B且垂直于l的直线y=x+3上,又圆心在y轴上,则圆心C2(0,3),
圆心到直线l:y=-x+3- 的距离
的距离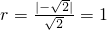 ,所以所求圆C2方程为:x2+(y-3)2=1,又AF∥l,F(c,0),A(0,b),所以有
,所以所求圆C2方程为:x2+(y-3)2=1,又AF∥l,F(c,0),A(0,b),所以有 ,即b=c,椭圆的离心率为
,即b=c,椭圆的离心率为 ;
;
(2)设∠EC2G=2a,则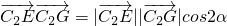 =cos2α=2cos2α-1,
=cos2α=2cos2α-1,
在Rt△PC2E中, ,由椭圆的几何性质有:
,由椭圆的几何性质有: ,
,
cosα=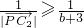 ,所以有
,所以有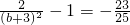 ,因b>0,所以b=2,
,因b>0,所以b=2,
所以椭圆的方程为 .
.
分析:(1)由圆心在y轴上的圆C2与斜率为1的直线l切于点B(-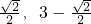 ),所以圆心在过B且垂直于l的直线y=x+3上,又圆心在y轴上,则圆心C2(0,3),圆心到直线l:y=-x+3-
),所以圆心在过B且垂直于l的直线y=x+3上,又圆心在y轴上,则圆心C2(0,3),圆心到直线l:y=-x+3- 的距离
的距离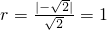 ,由此能求出椭圆的离心率.
,由此能求出椭圆的离心率.
(2)设∠EC2G=2a,则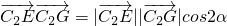 =cos2α=2cos2α-1,在Rt△PC2E中,
=cos2α=2cos2α-1,在Rt△PC2E中, ,由椭圆的几何性质有:
,由椭圆的几何性质有: ,由此能求出椭圆的方程.
,由此能求出椭圆的方程.
点评:本题考查椭圆的方程和椭圆的离心率的求法,解题时要认真审题,注意挖掘题设条件,合理运用椭圆性质,恰当进行等价转化.
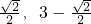 ),所以圆心在过B且垂直于l的直线y=x+3上,又圆心在y轴上,则圆心C2(0,3),
),所以圆心在过B且垂直于l的直线y=x+3上,又圆心在y轴上,则圆心C2(0,3),圆心到直线l:y=-x+3-
 的距离
的距离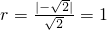 ,所以所求圆C2方程为:x2+(y-3)2=1,又AF∥l,F(c,0),A(0,b),所以有
,所以所求圆C2方程为:x2+(y-3)2=1,又AF∥l,F(c,0),A(0,b),所以有 ,即b=c,椭圆的离心率为
,即b=c,椭圆的离心率为 ;
;(2)设∠EC2G=2a,则
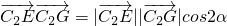 =cos2α=2cos2α-1,
=cos2α=2cos2α-1,在Rt△PC2E中,
 ,由椭圆的几何性质有:
,由椭圆的几何性质有: ,
,cosα=
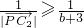 ,所以有
,所以有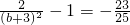 ,因b>0,所以b=2,
,因b>0,所以b=2,所以椭圆的方程为
 .
.分析:(1)由圆心在y轴上的圆C2与斜率为1的直线l切于点B(-
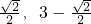 ),所以圆心在过B且垂直于l的直线y=x+3上,又圆心在y轴上,则圆心C2(0,3),圆心到直线l:y=-x+3-
),所以圆心在过B且垂直于l的直线y=x+3上,又圆心在y轴上,则圆心C2(0,3),圆心到直线l:y=-x+3- 的距离
的距离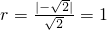 ,由此能求出椭圆的离心率.
,由此能求出椭圆的离心率.(2)设∠EC2G=2a,则
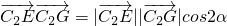 =cos2α=2cos2α-1,在Rt△PC2E中,
=cos2α=2cos2α-1,在Rt△PC2E中, ,由椭圆的几何性质有:
,由椭圆的几何性质有: ,由此能求出椭圆的方程.
,由此能求出椭圆的方程.点评:本题考查椭圆的方程和椭圆的离心率的求法,解题时要认真审题,注意挖掘题设条件,合理运用椭圆性质,恰当进行等价转化.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
 =1 (a>b>0)与双曲线C2:x2-
=1 (a>b>0)与双曲线C2:x2-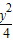 =1 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )
=1 有公共的焦点,C2的一条渐近线与以C1的长轴为直径的圆相交于A,B两点.若C1恰好将线段AB三等分,则( )

 +
+ =1(a>b>0)的长轴长为4,离心率为
=1(a>b>0)的长轴长为4,离心率为 ,F1、F2分别为其左右焦点.一动圆过点F2,且与直线x=-1相切.
,F1、F2分别为其左右焦点.一动圆过点F2,且与直线x=-1相切. 共线,
共线, 与
与 共线,且
共线,且 •
• =0,求四边形PMQN面积的最小值.
=0,求四边形PMQN面积的最小值. =1(a>b>0)的左、右焦点分别为F1、F2,其中F2也是抛物线C2:y2=4x的焦点,M是C1与C2在第一象限的交点,且
=1(a>b>0)的左、右焦点分别为F1、F2,其中F2也是抛物线C2:y2=4x的焦点,M是C1与C2在第一象限的交点,且
 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,直线l:x-y+
,直线l:x-y+ =0与椭圆C1相切.
=0与椭圆C1相切.