题目内容
我们用符号eiθ表示复数cosθ+isinθ,即eiθ=cosθ+isinθ(其中e是自然对数的底数,θ的单位是弧度),给出下面三个结论:
①2ei
=2i;②
=sinθ;③eiπ+1=0.以上结论中,正确结论的序号是( )
①2ei
| π |
| 2 |
| eiθ+e-iθ |
| 2 |
分析:由eiθ=cosθ+isinθ,知:①2e t
=2(cos
+isin
)=2i;②
=
[(cosθ+isinθ)+cos(-θ)+isin(-θ)]=cosθ;③eiπ+1=cosπ+isinπ+1=0.
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| eiθ+e-iθ |
| 2 |
| 1 |
| 2 |
解答:解:①∵eiθ=cosθ+isinθ,
∴2e t
=2(cos
+isin
)=2i,故①正确;
②∵eiθ=cosθ+isinθ,
∴
=
[(cosθ+isinθ)+cos(-θ)+isin(-θ)]=cosθ,故②不成立;
③∵eiθ=cosθ+isinθ,
∴eiπ+1=cosπ+isinπ+1=0,故③正确.
故选C.
∴2e t
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
②∵eiθ=cosθ+isinθ,
∴
| eiθ+e-iθ |
| 2 |
| 1 |
| 2 |
③∵eiθ=cosθ+isinθ,
∴eiπ+1=cosπ+isinπ+1=0,故③正确.
故选C.
点评:本题考查复数的代数形式的乘除运算,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
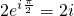 ;②
;②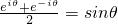 ;③eiπ+1=0.以上结论中,正确结论的序号是
;③eiπ+1=0.以上结论中,正确结论的序号是