题目内容
已知抛物线![]() ,点P(-1,0)是其准线与
,点P(-1,0)是其准线与![]() 轴的焦点,过P的直线
轴的焦点,过P的直线![]() 与抛物线C交于A、B两点。
与抛物线C交于A、B两点。
(1)当线段AB的中点在直线![]() 上时,求直线
上时,求直线![]() 的方程;
的方程;
(2)设F为抛物线C的焦点,当A为线段PB中点时,求△FAB的面积。
(Ⅰ) ![]() (Ⅱ)
(Ⅱ)![]()
解析:
(1)因为抛物线的准线为![]() ,所以
,所以![]() ,
,
抛物线方程为![]() 2分
2分
设![]() ,直线
,直线![]() 的方程为
的方程为![]() ,(依题意
,(依题意![]() 存在,且
存在,且![]() ≠0)
≠0)
与抛物线方程联立,消去![]() 得
得

![]() …………(*)
…………(*)
![]() ,
,![]() 4分
4分
所以AB中点的横坐标为![]() ,
,
即![]()
所以![]() 6分
6分
(此时(*)式判别式大于零)
所以直线![]() 的方程为
的方程为![]() 7分
7分
(2)因为A为线段PB中点,所以![]() 8分
8分
由A、B为抛物线上点,得![]() ,
,![]() 10分
10分
解得![]() ,
,![]() 11分
11分
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() 12分
12分
所以△FAB的面积![]()

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
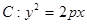 ,点P(-1,0)是其准线与
,点P(-1,0)是其准线与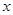 轴的焦点,过P的直线
轴的焦点,过P的直线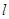 与抛物线C交于A、B两点.
与抛物线C交于A、B两点. 上时,求直线
上时,求直线 ,点P在此抛物线上,则P到直线
,点P在此抛物线上,则P到直线 和
和 轴的距离之和的最小值
轴的距离之和的最小值 B.
B. C.2 D.
C.2 D.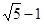
 通过点P(1,1),且在点Q(2,-1)处与直线
通过点P(1,1),且在点Q(2,-1)处与直线 相切,求实数
相切,求实数 的值.
的值.