题目内容
【题目】若函数
同时满足:
①对于定义域上的任意
,恒有
；
②对于定义域上的任意
,当
时,恒有
；
则称函数为“理想函数”.给出下列三个函数：（1）
（2）
（3）
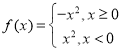，其中能被称为“理想函数”的有（ ）个.
A.1B.2C.3D.4
【答案】A
【解析】
满足①
为奇函数，满足②在定义域内是减函数，对（1）（2）（3）中的三个函数逐个判断，即可得结果.
对于①对于定义域上的任意
,恒有
；
则有
，故满足条件①为奇函数；
对于②对于定义域上的任意
,当
时，
不妨设
，恒有
，
，
故满足②条件的函数是在定义域内是减函数；
所以“理想函数”即为定义域内是减函数且为奇函数.
（1）
，在定义域不是减函数，故不是；
（2）
不是奇函数，故不是；
（3）
，
，所以为奇函数，
作出其图像，函数在定义域内是减函数，故为“理想函数”.
故选:A
【题目】2022年北京冬奥会的申办成功与“3亿人上冰雪”口号的提出，将冰雪这个冷项目迅速炒“热”．北京某综合大学计划在一年级开设冰球课程，为了解学生对冰球运动的兴趣，随机从该校一年级学生中抽取了100人进行调查，其中女生中对冰球运动有兴趣的占
，而男生有10人表示对冰球运动没有兴趣额．
（1）完成
列联表，并回答能否有
的把握认为“对冰球是否有兴趣与性别有关”？
有兴趣 | 没兴趣 | 合计 | |
男 | 55 | ||
女 | |||
合计 |
（2）若将频率视为概率，现再从该校一年级全体学生中，采用随机抽样的方法每次抽取1名学生，抽取5次，记被抽取的5名学生中对冰球有兴趣的人数为
，若每次抽取的结果是相互独立的，求的分布列，期望和方差．
附表：
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】某企业常年生产一种出口产品，根据预测可知，进入
世纪以来，该产品的产量平稳增长．记
年为第
年，且前
年中，第
年与年产量
万件之间的关系如下表所示：
|
|
|
|
|
|
|
|
|
|
若近似符合以下三种函数模型之一：
，
，
．
(1)找出你认为最适合的函数模型，并说明理由，然后选取其中你认为最适合的数据求出相应的解析式；
(2)因遭受某国对该产品进行反倾销的影响，
年的年产量比预计减少
，试根据所建立的函数模型，确定年的年产量．
