题目内容
等差数列{an}中,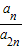 是一个与n无关的常数,则该常数的可能值的集合为( )
是一个与n无关的常数,则该常数的可能值的集合为( )A.1
B.
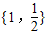
C.
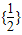
D.
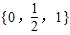
【答案】分析:先根据等差数列的通项公式计算出an=a1+(n-1)d与a2n=a1+(2n-1)d,进而表达出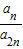 ,再结合题中的条件以及分式的特征可得答案.
,再结合题中的条件以及分式的特征可得答案.
解答:解:由题意可得:
因为数列{an}是等差数列,
所以设数列{an}的通项公式为:an=a1+(n-1)d,则a2n=a1+(2n-1)d,
所以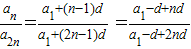 .
.
因为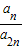 是一个与n无关的常数,
是一个与n无关的常数,
所以a1-d=0或d=0,
所以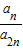 可能是1或
可能是1或 .
.
故选B.
点评:解决此类问题的关键是熟练掌握等差数列的通项公式,以及熟练掌握分式的性质,
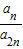 ,再结合题中的条件以及分式的特征可得答案.
,再结合题中的条件以及分式的特征可得答案.解答:解:由题意可得:
因为数列{an}是等差数列,
所以设数列{an}的通项公式为:an=a1+(n-1)d,则a2n=a1+(2n-1)d,
所以
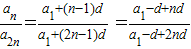 .
.因为
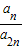 是一个与n无关的常数,
是一个与n无关的常数,所以a1-d=0或d=0,
所以
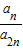 可能是1或
可能是1或 .
.故选B.
点评:解决此类问题的关键是熟练掌握等差数列的通项公式,以及熟练掌握分式的性质,

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目