题目内容
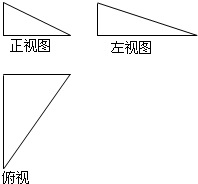 (2012•葫芦岛模拟)一个三棱锥的三视图如图所示,其正视图、左视图、俯视图的面积分别是2,4,8,则这个几何体的体积为
(2012•葫芦岛模拟)一个三棱锥的三视图如图所示,其正视图、左视图、俯视图的面积分别是2,4,8,则这个几何体的体积为8
| ||
| 3 |
8
| ||
| 3 |
分析:由三视图知,此三棱锥存在同一点出发的三条棱,可设出此三条棱的长度,根据面积公式与体积公式建立方程即可求出该几何体的体积
解答:解:由题意,此几何体是一个有公共点的三个面是直角三角形的棱锥,可设同一点出发的三条互相垂直的棱的长度为a,b,c,
∵由题意正视图、左视图、俯视图的面积分别是2,4,8
∴ab=4,bc=8,ca=16,
∴几何体的体积V=
abc=
×
=
故答案为
∵由题意正视图、左视图、俯视图的面积分别是2,4,8
∴ab=4,bc=8,ca=16,
∴几何体的体积V=
| 1 |
| 6 |
| 1 |
| 6 |
| 4×8×16 |
8
| ||
| 3 |
故答案为
8
| ||
| 3 |
点评:本题考查由视图还原几何体,体积公式,属于立体几何中的基础题型,也是近年高考的热点,熟练掌握三视图的规则是解题的关键

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
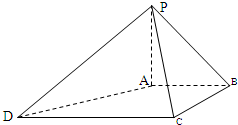 (2012•葫芦岛模拟)在四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AB⊥BC,PA=AB=BC=
(2012•葫芦岛模拟)在四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AB⊥BC,PA=AB=BC=