题目内容
已知![]() 是奇函数.
是奇函数.
(1)求![]() 的值;
的值;
(2)判断并证明![]() 在
在![]() 上的单调性;
上的单调性;
(3)若关于![]() 的方程
的方程![]() 在
在![]() 上有解,求
上有解,求![]() 的取值范围.
的取值范围.
解:(1)因为![]() 是奇函数,故对定义域内的x,都有
是奇函数,故对定义域内的x,都有![]()
即![]() ,
,
即![]() ,于是
,于是![]() .…………………3分
.…………………3分
(2)![]() 在
在![]() 上的单调递减. .……………………………………………………2分
上的单调递减. .……………………………………………………2分
对任意的![]()
![]()
故![]()
即![]() 在
在![]() 上的单调递减. . .……………………………………………………3分
上的单调递减. . .……………………………………………………3分
(3)解法一:方程![]() 可化为:
可化为:
![]() ,令
,令![]()
于是![]() 在
在![]() 上有解………………………………………..2分
上有解………………………………………..2分
设![]()
(1)![]() 在
在![]() 上有两个零点(可重合),令
上有两个零点(可重合),令 无解.
无解.
(2)![]() 在
在![]() 上有1个零点,令
上有1个零点,令![]() ,得
,得![]()
综上得![]() ……………………………………………………………………2分
……………………………………………………………………2分
解法二:方程![]() 可化为:
可化为:
![]() ,令
,令![]()
于是![]() ,………………………………………..2分
,………………………………………..2分
则![]()
![]() 的值域为
的值域为![]() ,故
,故![]() .…………………………2分
.…………………………2分

练习册系列答案
相关题目
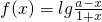 是奇函数.
是奇函数. 是奇函数.
是奇函数.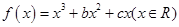 ,已知
,已知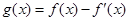 是奇函数。
是奇函数。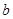 、
、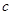 的值。
的值。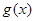 的单调区间与极值。
的单调区间与极值。