题目内容
如图1-2-6,某炮兵阵地位于A点,两观察所分别位于C、D两点.已知△ACD为正三角形,且DC=
km,当目标出现在B时,测得∠CDB=45°，∠BCD=75°,求炮兵阵地与目标的距离是多少？(精确到0.01 km) 
图1-2-6
解:由B=180°-∠BCD-∠CDB=60°，
在△BCD中，由正弦定理，得BD=
=(
).
在△ABD中,∠ADB=45°+60°=105°，
由余弦定理,得
AB2=AD2+BD2-2AD·BD·cos105°=3+
(
)2+2×
×
(
)×
(
)=5+
，∴AB=
≈2.91.
∴炮兵阵地与目标的距离是2.91 km.
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
如图，建立平面直角坐标系x0y，x轴在地平面上，y轴垂直于地平面，单位长度为1千米．某炮位于坐标原点．
如图，建立平面直角坐标系x0y，x轴在地平面上，y轴垂直于地平面，单位长度为1千米．某炮位于坐标原点．
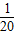（1+k2）x2（k＞0）表示的曲线上，其中k与发射方向有关．炮弹的射程是指炮弹落地点的横坐标．
（1+k2）x2（k＞0）表示的曲线上，其中k与发射方向有关．炮弹的射程是指炮弹落地点的横坐标．
（1+k2）x2（k＞0）表示的曲线上，其中k与发射方向有关．炮弹的射程是指炮弹落地点的横坐标．