题目内容
(本小题满分l2分)
已知数列![]() 满足,
满足,![]()
![]() ,且
,且![]() .(
.(![]() N*)
N*)
(I)求数列![]() 的通项公式;
的通项公式;
(II)若![]() =
=![]() 试问数列
试问数列![]() 中是否存在三项能按某种顺序构成等差数列?
中是否存在三项能按某种顺序构成等差数列?
若存在,求出满足条件的等差数列,若不存在;说明理由.
(本小题满分12分)
解:(I)由![]() ,
,![]() 知,
知,
当![]() 为偶数时,
为偶数时,![]() ;当
;当![]() 为奇数时,
为奇数时,![]() ;……………2分
;……………2分
由![]() ,得
,得![]() ,即
,即![]() ,
,
所以![]() ,
,
即数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列
为公比的等比数列
所以,![]() ,
,![]() ,
,
故 (
(![]() N*)…………………5分
N*)…………………5分
(II)由(I)知![]()
![]() ,
,
则对于任意的![]() ,
,![]() .………………7分
.………………7分
假设数列![]() 中存在三项
中存在三项![]() (
(![]() )成等差数列,
)成等差数列,
则![]() ,即只能有
,即只能有![]() 成立,
成立,
所以![]() ,
,![]() ………………9分
………………9分
所以,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以![]() 是偶数,
是偶数,![]() 是奇数,而偶数与奇数不可能相等,
是奇数,而偶数与奇数不可能相等,
因此数列![]() 中任意三项不可能成等差数列.…………………12分
中任意三项不可能成等差数列.…………………12分

练习册系列答案
相关题目
 ,bn+1=-
,bn+1=- Sn(n∈N*).
Sn(n∈N*). +
+ +…+
+…+ ,求Tn的表达式
,求Tn的表达式 ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
. 为直径的圆经过焦点
为直径的圆经过焦点 .
. :函数
:函数 (
( )的值域是
)的值域是 ;命题
;命题 :指数函数
:指数函数 在
在 上是减函数.若命题“
上是减函数.若命题“ 的范围.
的范围. 并且与曲线
并且与曲线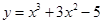 相切的直线方程.
相切的直线方程.