题目内容
已知M=
,α=
,试计算:M10α
选修4-4 参数方程与极坐标
过点P(-3,0)且倾斜角为30°直线和曲线
(t为参数)相交于A、B两点.求线段AB的长.
|
|
选修4-4 参数方程与极坐标
过点P(-3,0)且倾斜角为30°直线和曲线
|
(1)矩阵M的特征多项式为:f(λ)=λ2-λ-2=0,λ1=-1,λ2=2.
λ1=-1对应的一个特征向量为:
=
,λ2=2对应的一个特征向量为:
=
.(4分)
设a=m
+n
,即
=m
+n
,∴
解得
.(5分)
M10α=3(λ1)10
+(-2)(λ2)10
=3(-1)10
+(-2)10
=
或
.
(2)直线的参数方程为
(s 为参数),曲线
可以化为 x2-y2=4.
将直线的参数方程代入上式,得 s2-6
+ 10 = 0.
设A、B对应的参数分别为 s1,s2,∴s1+ s2= 6
,s1•s2=10.
∴AB=|s1-s2|=
=2
.
λ1=-1对应的一个特征向量为:
| α1 |
|
| α2 |
|
设a=m
| a1 |
| a2 |
|
|
|
|
|
M10α=3(λ1)10
| α1 |
| α2 |
|
|
|
|
(2)直线的参数方程为
|
|
将直线的参数方程代入上式,得 s2-6
| 3 |
设A、B对应的参数分别为 s1,s2,∴s1+ s2= 6
| 3 |
∴AB=|s1-s2|=
| (s1- s2)2-4s1s2 |
| 17 |

练习册系列答案
相关题目
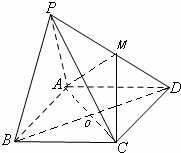 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2